library(tidyverse)
library(caret)
library(glmnet)
library(ROCR)Table of Content
- 1 Introduction
- 2 Load and prepare the dataset
- 3 Train the model
- 4 Manual calculation of some key figures
- 4.1 p value of Thal7
- 4.2 Model deviance
- 4.3 Null deviance
- 4.4 Pseudo R2
- 4.5 Model deviance residuals
- 5 Test set performance
- 6 Regularization with lasso
- 6.1 Classification accuracy for the train set
- 6.2 Classification accuracy for the test set
- 7 Classification metrics
- 8 Conclusion
1 Introduction
In my last post (“Machine Learning - Predictions with linear regressions”) I treated the topic of predicting numerical values using regression models. However, regression models are also suitable for making classifications. This can be done by means of so-called logistic regression models. Logistic regression belongs to a class of models known as Generalized Linear Models.
Subsequently, logistical regression will be used to determine the presence of heart disease.
For this post the dataset Statlog (Heart) from the UCI- Machine Learning Repository platform “UCI” was used.
2 Load and prepare the dataset
url = "http://archive.ics.uci.edu/ml/machine-learning-databases/statlog/heart/heart.dat"
heart = read.table(url)names(heart) <- c("AGE", "SEX", "CHESTPAIN", "RESTBP", "CHOL",
"SUGAR", "ECG", "MAXHR", "ANGINA", "DEP", "EXERCISE", "FLUOR",
"THAL", "OUTPUT")
glimpse(heart)## Observations: 270
## Variables: 14
## $ AGE <dbl> 70, 67, 57, 64, 74, 65, 56, 59, 60, 63, 59, 53, 44, ...
## $ SEX <dbl> 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1...
## $ CHESTPAIN <dbl> 4, 3, 2, 4, 2, 4, 3, 4, 4, 4, 4, 4, 3, 1, 4, 4, 4, 4...
## $ RESTBP <dbl> 130, 115, 124, 128, 120, 120, 130, 110, 140, 150, 13...
## $ CHOL <dbl> 322, 564, 261, 263, 269, 177, 256, 239, 293, 407, 23...
## $ SUGAR <dbl> 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1...
## $ ECG <dbl> 2, 2, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 0, 2, 0, 0, 2...
## $ MAXHR <dbl> 109, 160, 141, 105, 121, 140, 142, 142, 170, 154, 16...
## $ ANGINA <dbl> 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1...
## $ DEP <dbl> 2.4, 1.6, 0.3, 0.2, 0.2, 0.4, 0.6, 1.2, 1.2, 4.0, 0....
## $ EXERCISE <dbl> 2, 2, 1, 2, 1, 1, 2, 2, 2, 2, 2, 1, 1, 2, 1, 2, 2, 3...
## $ FLUOR <dbl> 3, 0, 0, 1, 1, 0, 1, 1, 2, 3, 0, 0, 0, 2, 1, 0, 2, 0...
## $ THAL <dbl> 3, 7, 7, 7, 3, 7, 6, 7, 7, 7, 7, 7, 3, 3, 3, 3, 7, 7...
## $ OUTPUT <int> 2, 1, 2, 1, 1, 1, 2, 2, 2, 2, 1, 1, 1, 2, 1, 1, 2, 2...The Chestpain, Thal and ECG features are all categorical features. Therefore we have to convert them as well as the dependent variable Output (we need class labes of 0 and 1).
heart$CHESTPAIN = factor(heart$CHESTPAIN)
heart$ECG = factor(heart$ECG)
heart$THAL = factor(heart$THAL)
heart$EXERCISE = factor(heart$EXERCISE)
heart$OUTPUT = heart$OUTPUT - 13 Train the model
set.seed(987954)
heart_sampling_vector <-
createDataPartition(heart$OUTPUT, p = 0.85, list = FALSE)
heart_train <- heart[heart_sampling_vector,]
heart_train_labels <- heart$OUTPUT[heart_sampling_vector]
heart_test <- heart[-heart_sampling_vector,]
heart_test_labels <- heart$OUTPUT[-heart_sampling_vector]
heart_model <- glm(OUTPUT ~ ., data = heart_train, family = binomial("logit"))
summary(heart_model)##
## Call:
## glm(formula = OUTPUT ~ ., family = binomial("logit"), data = heart_train)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.7137 -0.4421 -0.1382 0.3588 2.8118
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -7.946051 3.477686 -2.285 0.022321 *
## AGE -0.020538 0.029580 -0.694 0.487482
## SEX 1.641327 0.656291 2.501 0.012387 *
## CHESTPAIN2 1.308530 1.000913 1.307 0.191098
## CHESTPAIN3 0.560233 0.865114 0.648 0.517255
## CHESTPAIN4 2.356442 0.820521 2.872 0.004080 **
## RESTBP 0.026588 0.013357 1.991 0.046529 *
## CHOL 0.008105 0.004790 1.692 0.090593 .
## SUGAR -1.263606 0.732414 -1.725 0.084480 .
## ECG1 1.352751 3.287293 0.412 0.680699
## ECG2 0.563430 0.461872 1.220 0.222509
## MAXHR -0.013585 0.012873 -1.055 0.291283
## ANGINA 0.999906 0.525996 1.901 0.057305 .
## DEP 0.196349 0.282891 0.694 0.487632
## EXERCISE2 0.743530 0.560700 1.326 0.184815
## EXERCISE3 0.946718 1.165567 0.812 0.416655
## FLUOR 1.310240 0.308348 4.249 2.15e-05 ***
## THAL6 0.304117 0.995464 0.306 0.759983
## THAL7 1.717886 0.510986 3.362 0.000774 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 315.90 on 229 degrees of freedom
## Residual deviance: 140.36 on 211 degrees of freedom
## AIC: 178.36
##
## Number of Fisher Scoring iterations: 64 Manual calculation of some key figures
4.1 p value of Thal7
pnorm(3.362 , lower.tail = F) * 2## [1] 0.00077380124.2 Model deviance
log_likelihoods <- function(y_labels, y_probs) {
y_a <- as.numeric(y_labels)
y_p <- as.numeric(y_probs)
y_a * log(y_p) + (1 - y_a) * log(1 - y_p)
}
dataset_log_likelihood <- function(y_labels, y_probs) {
sum(log_likelihoods(y_labels, y_probs))
}
# ---
deviances <- function(y_labels, y_probs) {
-2 * log_likelihoods(y_labels, y_probs)
}
dataset_deviance <- function(y_labels, y_probs) {
sum(deviances(y_labels, y_probs))
}
model_deviance <- function(model, data, output_column) {
y_labels = data[[output_column]]
y_probs = predict(model, newdata = data, type = "response")
dataset_deviance(y_labels, y_probs)
}
model_deviance(heart_model, data = heart_train, output_column = "OUTPUT")## [1] 140.35614.3 Null deviance
null_deviance <- function(data, output_column) {
y_labels <- data[[output_column]]
y_probs <- mean(data[[output_column]])
dataset_deviance(y_labels, y_probs)
}
null_deviance(data = heart_train, output_column = "OUTPUT")## [1] 315.90234.4 Pseudo R2
model_pseudo_r_squared <- function(model, data, output_column) {
1 - ( model_deviance(model, data, output_column) /
null_deviance(data, output_column) )
}
model_pseudo_r_squared(heart_model, data = heart_train, output_column = "OUTPUT")## [1] 0.5556977model_chi_squared_p_value <- function(model, data, output_column) {
null_df <- nrow(data) - 1
model_df <- nrow(data) - length(model$coefficients)
difference_df <- null_df - model_df
null_deviance <- null_deviance(data, output_column)
m_deviance <- model_deviance(model, data, output_column)
difference_deviance <- null_deviance - m_deviance
pchisq(difference_deviance, difference_df,lower.tail = F)
}
model_chi_squared_p_value(heart_model, data = heart_train, output_column = "OUTPUT")## [1] 7.294219e-28Our logistic mode is said to expain roughly 56% of the null deviance with an p value of < .001.
4.5 Model deviance residuals
model_deviance_residuals <- function(model, data, output_column) {
y_labels = data[[output_column]]
y_probs = predict(model, newdata = data, type = "response")
residual_sign = sign(y_labels - y_probs)
residuals = sqrt(deviances(y_labels, y_probs))
residual_sign * residuals
}
summary(model_deviance_residuals(heart_model, data = heart_train, output_column = "OUTPUT"))## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -2.71369 -0.44214 -0.13823 -0.02765 0.35875 2.811785 Test set performance
train_predictions <- predict(heart_model, newdata = heart_train, type = "response")
train_class_predictions <- as.numeric(train_predictions > 0.5)
mean(train_class_predictions == heart_train$OUTPUT)## [1] 0.8869565The classification accuracy on the training set is 89%.
test_predictions = predict(heart_model, newdata = heart_test, type = "response")
test_class_predictions = as.numeric(test_predictions > 0.5)
mean(test_class_predictions == heart_test$OUTPUT)## [1] 0.775The classification accuracy on the test set is 78%.
6 Regularization with lasso
heart_train_mat <- model.matrix(OUTPUT ~ ., heart_train)[,-1]
lambdas <- 10 ^ seq(8, -4, length = 250)
heart_models_lasso <- glmnet(heart_train_mat, heart_train$OUTPUT, alpha = 1, lambda = lambdas, family = "binomial")
lasso.cv <- cv.glmnet(heart_train_mat, heart_train$OUTPUT,
alpha = 1,lambda = lambdas, family = "binomial")
lambda_lasso <- lasso.cv$lambda.min
lambda_lasso## [1] 0.01181107predict(heart_models_lasso, type = "coefficients", s = lambda_lasso)## 19 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) -4.702476656
## AGE .
## SEX 0.982354604
## CHESTPAIN2 0.050583269
## CHESTPAIN3 .
## CHESTPAIN4 1.481502102
## RESTBP 0.012612051
## CHOL 0.003912907
## SUGAR -0.536400517
## ECG1 .
## ECG2 0.321026773
## MAXHR -0.010563953
## ANGINA 0.795431862
## DEP 0.213059195
## EXERCISE2 0.320076517
## EXERCISE3 0.012296570
## FLUOR 0.925047313
## THAL6 0.066580841
## THAL7 1.484011300We can see that a number of our features have effectively been removed from the model because their coefficients are zero. Let’s use this new model to measure the classification accuracy on our training and test sets. We observe that in both cases, we get slighty better performance.
6.1 Classification accuracy for the train set
lasso_train_predictions <- predict(heart_models_lasso, s = lambda_lasso, newx = heart_train_mat, type = "response")
lasso_train_class_predictions <- as.numeric(lasso_train_predictions > 0.5)
mean(lasso_train_class_predictions == heart_train$OUTPUT)## [1] 0.89130436.2 Classification accuracy for the test set
heart_test_mat <- model.matrix(OUTPUT ~ ., heart_test)[,-1]
lasso_test_predictions <- predict(heart_models_lasso, s = lambda_lasso, newx = heart_test_mat, type = "response")
lasso_test_class_predictions <- as.numeric(lasso_test_predictions > 0.5)
mean(lasso_test_class_predictions == heart_test$OUTPUT)## [1] 0.7757 Classification metrics
In our case a binary confusion matrix can be used to compute a number of other useful performance metrics for our data, such as precision, recall and the specificity.
confusion_matrix <- table(predicted = train_class_predictions, actual = heart_train$OUTPUT)
confusion_matrix## actual
## predicted 0 1
## 0 118 16
## 1 10 86precision <- confusion_matrix[2, 2] / sum(confusion_matrix[2,])
precision## [1] 0.8958333recall <- confusion_matrix[2, 2] / sum(confusion_matrix[,2])
recall## [1] 0.8431373(f = 2 * precision * recall / (precision + recall))## [1] 0.8686869Recall is also known as the true positive rate.
specificity <- confusion_matrix[1,1]/sum(confusion_matrix[1,])
specificity## [1] 0.880597Specificity is the false negative rate.
Ideally, what we would like is a visual way to assess the effect of changing the threshold (we have used 0.5 so far) on our performance metrics, and the precision recall curve is one such useful plot.
train_predictions <- predict(heart_model, newdata = heart_train, type = "response")
pred <- prediction(train_predictions, heart_train$OUTPUT)
perf <- performance(pred, measure = "prec", x.measure = "rec")
plot(perf)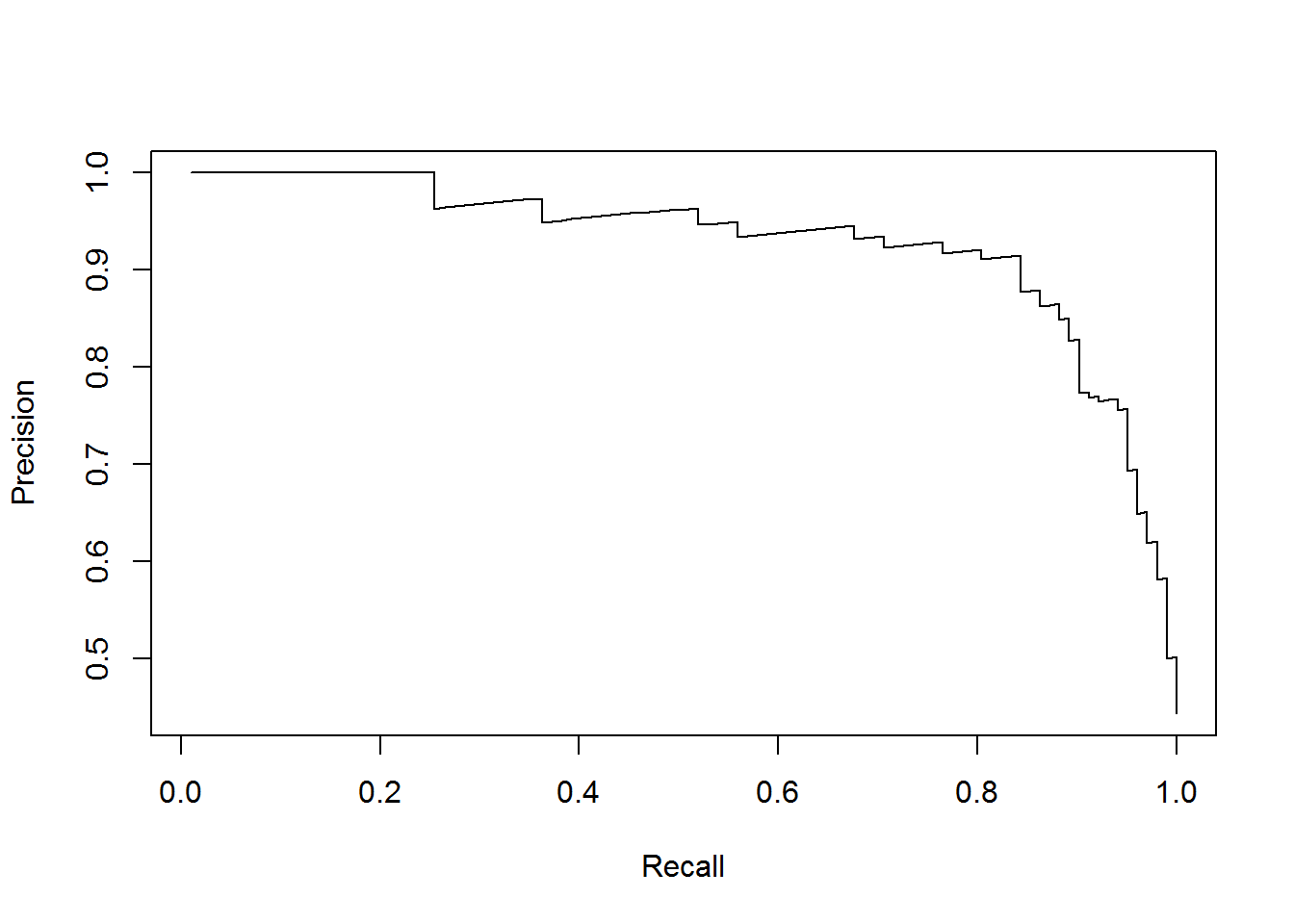
The plot shows us, that, to obtain values of recall above 0.8, we’ll have to sacrifice precision quite abruptly. Therefore it is usefull to create a data frame of cutoff values, which are the threshold values for which precision and recall change in our data, along with their corresponding precision and recall values.
For example, we want to find a suitable threshold so that we have at least 90% recall and 80% precision.
thresholds <- data.frame(cutoffs = perf@alpha.values[[1]], recall = perf@x.values[[1]], precision = perf@y.values[[1]])
subset(thresholds,(recall > 0.9) & (precision > 0.8))## cutoffs recall precision
## 112 0.3491857 0.9019608 0.8288288
## 113 0.3472740 0.9019608 0.8214286
## 114 0.3428354 0.9019608 0.8141593
## 115 0.3421438 0.9019608 0.8070175As we can see, a threshold of 0.35 will satisfy our requirements.
8 Conclusion
We have seen how it is possible to make classifications with a logistic regression and to increase the predictive accuracy of this models.
Source
Miller, J. D., & Forte, R. M. (2017). Mastering Predictive Analytics with R. Packt Publishing Ltd.