library(tidyverse)
library(psych)
library(readxl)
library(GPArotation)

BigFive <- read_excel("BigFive.xlsx")

Table of Content

1 Introduction
2 Determination of the number of factors
3 Execution of the factor analysis
4 Conclusion

1 Introduction

Mithilfe der exploratorischen Faktorenanalyse kann aus den Beobachtungen vieler manifester Variablen (beispielsweise Items eines Fragebogens) auf wenige zugrunde liegende latente Variablen geschlossen werden. Diese latenten Variablen werden Faktoren genannt. Eine Faktorenanalyse führt demnach zu einer Reduktion der Variablen auf wenige, den manifesten Variablen zugrunde liegende, Faktoren.

Für die exemplarische Durchführung einer Faktorenanalyse wurde der Datensatz BigFive verwendet. Eine Kopie des Datensatzes ist unter https://drive.google.com/open?id=1bD6qeHLfkPBQTosJZFug0PthTRFjbNf0 abrufbar.

2 Determination of the number of factors

Die exploratorische Faktorenanalyse ist ein Verfahren das angewendet wird, wenn in einem Datensatz nach einer noch unbekannten korrelativen Struktur gesucht werden soll. Sie gehört somit in die Gruppe der strukturentdeckenden Verfahren. Nachfolgend soll die Anzahl an Faktoren für den Datensatz BigFive bestimmt werden.

fa.parallel(BigFive, fa="fa")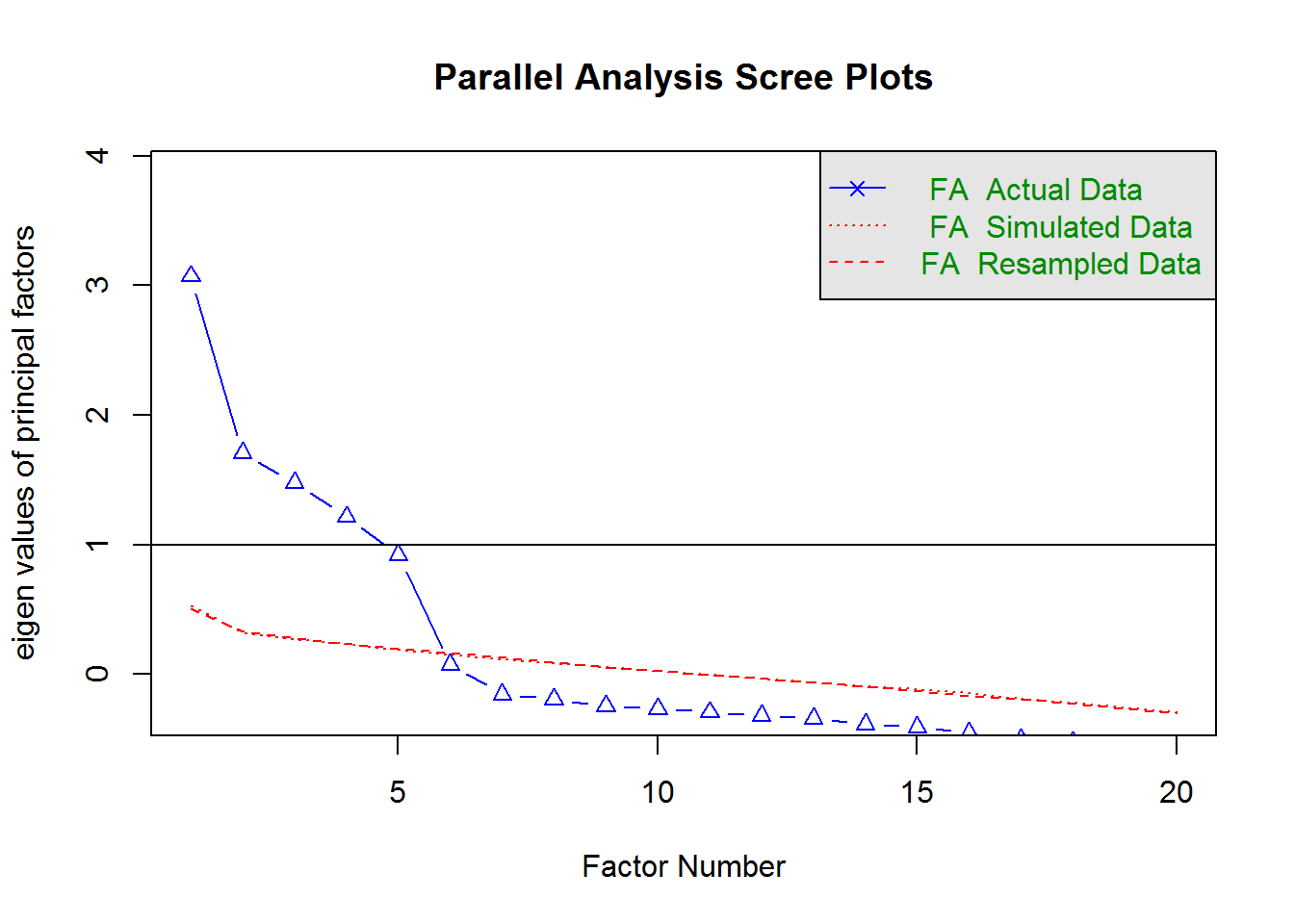

## Parallel analysis suggests that the number of factors =  5  and the number of components =  NA

Die fa.parallel Funktion enthält zwei Argumente. Das erste Argument ist der zu untersuchende Datensatz und das zweite Argument legt die Extraktionsmethode fest. Die Bezeichnung fa=“fa” steht dabei für “Hauptachsenanalyse”. Des Weiteren wäre die Auswahl der “Hauptkomponentenanalyse” (fa=“pc”) möglich gewesen. Diese zählt allerdings im strengen Sinne nicht zur Faktorenanalyse.

Eigenwert-Kriterium

In dem von uns erstellten Diagramm ist der Eigenwertverlauf abgebildet. Dabei stellt jedes Kreuz den Eigenwert eines gefundenen Faktors dar. Der größte gefundene Wert wird auf der x-Achse als erstes (ganz links) abgebildet. Geht man demnach auf der x-Achse weiter nach rechts, werden die Eigenwerte immer kleiner. Der Eigenwert eines jeden Faktors sagt aus, wie viel Varianz dieser Faktor an der Gesamtvarianz aller Items aufklärt. Es sollten nur Faktoren extrahiert werden, deren Eigenwert größer 1 liegt. In der Abbildung ist erkennbar, dass 4 Faktoren oberhalb der Geraden (Eigenwert von 1) liegen. Dem Eigenwert-Kriterium nach, besteht der Datensatz BigFive aus 4 Faktoren. Aus der Literatur ist allerdings bekannt, dass das Fünf-Faktoren-Modell (FFM) aus 5 Hauptdimensionen der Persönlichkeit besteht. Dass diese nicht alle nach dem Eigenwert-Kriterium identifiziert werden liegt daran, dass diese Methode recht willkürlich ist und sowohl zur Über- als auch Unterfaktorisierung führen kann. Aus diesem Grund wird meistens der Scree-Test zusätzlich hinzugezogen.

Scree-Test

Der Scree-Test ist kein herkömmlicher statistischer Test wie der T-Test oder ähnliches. Er ist mehr eine graphische Überprüfung des Screeplots (das erstellte Diagramm). Dabei wird nach einer Stelle nahe dem Wert 1 im Eigenwertverlauf gesucht, an der die Kurve plötzlich nach unten wegknickt. Diese Stelle wird meistens auch “Ellbogen” genannt und ist nach dem 5ten Faktor zu finden. Berücksichtigt man zusätzlich zum Eigenwert-Kriterium den Scree-Test, so lassen sich 5 Faktoren für den Datensatz BigFive bestimmen.

3 Execution of the factor analysis

Da nun die Anzahl der zu extrahierenden Faktoren festgelegt ist, kann die eigentliche Faktorenanalyse durchgeführt werden. Dabei sind erneut zwei Entscheidungen zu treffen:

Wahl der Extraktionsmethode: diese kann mithilfe der Maximum-Likelihood-Faktorenanalyse oder der Hauptachsenanalyse durchgeführt werden.
Wahl der Rotationsmethode: hierbei steht die orthogonale Rotation (die Faktoren dürfen nicht korrelieren) oder die oblique Rotation (die Faktoren dürfen korrelieren) zur Verfügung.

Im folgenden Beispiel soll eine Maximum-Likelihood-Faktorenanalyse mit Promax-Rotation durchgeführt werden.

fa.ml <- fa(BigFive, 5, fm="ml", rotate = "promax")

Die Funktion beinhaltet 4 Argumente. BigFive ist der Name des Datensatzes, in dem die zu analysierenden Variablen enthalten sind. 5 ist die Anzahl der zu extrahierenden Faktoren, welche im vorherigen Kapitel bestimmt worden sind. fm ist die gewünschte Extraktionsmethode. Dabei steht ml für Maximum Likelihood. rotate ist die gewünschte Rotationsmethode, wobei promax eine oblique Methode der Rotation ist.

Eine schöne Übersicht der Ergebnisse, lässt sich mit der print Funktion darstellen. Mit dem Zusatzargument digits=2 werden alle Zahlen auf zwei Nachkommastellen gerundet und mit cut=.3 werden nur Faktorladungen größer 0,30 angezeigt. Mit sort=TRUE werden alle Items, die auf den selben Faktor laden, in der Tabelle direkt untereinander gestellt.

print(fa.ml, digits = 2, cut = .3, sort = TRUE)

## Factor Analysis using method =  ml
## Call: fa(r = BigFive, nfactors = 5, rotate = "promax", fm = "ml")
## Standardized loadings (pattern matrix) based upon correlation matrix
##           item   ML2   ML1   ML5   ML3   ML4   h2   u2 com
## BigFive07    7  0.91                         0.78 0.22 1.0
## BigFive03    3  0.86                         0.75 0.25 1.0
## BigFive20   20  0.73                         0.54 0.46 1.0
## BigFive11   11  0.53                         0.34 0.66 1.3
## BigFive09    9        0.95                   0.83 0.17 1.1
## BigFive05    5        0.91                   0.77 0.23 1.1
## BigFive18   18        0.50                   0.34 0.66 1.2
## BigFive14   14        0.47                   0.27 0.73 1.1
## BigFive08    8              0.73             0.51 0.49 1.1
## BigFive15   15              0.70             0.43 0.57 1.1
## BigFive17   17              0.67             0.50 0.50 1.1
## BigFive02    2              0.61             0.47 0.53 1.2
## BigFive13   13                    0.84       0.66 0.34 1.1
## BigFive16   16                    0.72       0.50 0.50 1.1
## BigFive01    1                    0.62       0.41 0.59 1.0
## BigFive06    6                    0.55       0.40 0.60 1.4
## BigFive04    4                          0.77 0.63 0.37 1.2
## BigFive10   10                          0.76 0.58 0.42 1.1
## BigFive12   12                          0.52 0.34 0.66 1.6
## BigFive19   19                          0.52 0.29 0.71 1.1
## 
##                        ML2  ML1  ML5  ML3  ML4
## SS loadings           2.40 2.15 2.05 2.02 1.75
## Proportion Var        0.12 0.11 0.10 0.10 0.09
## Cumulative Var        0.12 0.23 0.33 0.43 0.52
## Proportion Explained  0.23 0.21 0.20 0.19 0.17
## Cumulative Proportion 0.23 0.44 0.64 0.83 1.00
## 
##  With factor correlations of 
##      ML2   ML1   ML5  ML3   ML4
## ML2 1.00  0.23  0.26 0.09  0.02
## ML1 0.23  1.00  0.16 0.27 -0.08
## ML5 0.26  0.16  1.00 0.31 -0.03
## ML3 0.09  0.27  0.31 1.00  0.00
## ML4 0.02 -0.08 -0.03 0.00  1.00
## 
## Mean item complexity =  1.1
## Test of the hypothesis that 5 factors are sufficient.
## 
## The degrees of freedom for the null model are  190  and the objective function was  7.45 with Chi Square of  3525.61
## The degrees of freedom for the model are 100  and the objective function was  0.54 
## 
## The root mean square of the residuals (RMSR) is  0.03 
## The df corrected root mean square of the residuals is  0.04 
## 
## The harmonic number of observations is  481 with the empirical chi square  165.99  with prob <  3.8e-05 
## The total number of observations was  482  with Likelihood Chi Square =  252.1  with prob <  4.1e-15 
## 
## Tucker Lewis Index of factoring reliability =  0.913
## RMSEA index =  0.057  and the 90 % confidence intervals are  0.048 0.065
## BIC =  -365.7
## Fit based upon off diagonal values = 0.98
## Measures of factor score adequacy             
##                                                    ML2  ML1 ML5  ML3  ML4
## Correlation of (regression) scores with factors   0.94 0.95 0.9 0.91 0.89
## Multiple R square of scores with factors          0.89 0.90 0.8 0.82 0.79
## Minimum correlation of possible factor scores     0.79 0.80 0.6 0.64 0.58

Standardized loadings (pattern matrix) based upon correlation matrix

Die erste Tabelle enthält die Faktorladungen der einzelnen Variablen auf den Faktoren ML1 bis ML5. Sehr erstrebenswert ist es, wenn die Variablen möglichst hoch auf einem und möglichst gering auf allen anderen Faktoren laden. Die Kommunalität (h2) sagt aus, wie viel Prozent der Varianz dieses Items durch alle fünf Faktoren erklärt wird. Dahingegen drückt der Uniqueness-Wert (u2) den Anteil der Varianz aus, der nicht durch die Faktoren erklärt wird. Je höher u2 ist, desto weniger hat das Item mit den anderen Items gemeinsam. Der Komplexitätswert (com) erklärt, wie viele latente Faktoren notwendig sind, um die Varianz dieses Items zu erklären. Erstrebenswert ist hierbei, dass alle Items einen com-Wert nahe 1 besitzen, denn dies entspricht einer Einfachstruktur. Dies bedeutet, dass die Items eine hohe Ladung auf genau einem einzigen Faktor haben und niedrige Ladungen auf allen anderen Faktoren besitzen.

SS loadings

Die nächste Tabelle zeigt die quadrierten und aufsummierten Ladungen der einzelnen Faktoren. Die Zeile Proportion Var enthält den Anteil der Varianz dieses Faktors an der Gesamtvarianz. In der darunterliegenden Zeile Cumulative Var werden diese Werte addiert. Hier erkennt man, dass die fünf Faktoren zusammen 52% der Gesamtvarianz aufklären. In der Zeile Proportion Explained steht, wie viel jeder Faktor zur erklärten Varianz (die 52%) beiträgt.

With factor correlations of

Diese Tabelle enthält die Interfaktor-Korrelationen. Man sieht, dass fast alle Korrelationen klein bis mittelstark ausfallen.

Anschließend werden noch eine Reihe von Fit-Statistiken ausgegeben, auf die in diesem Post nicht weiter eingegangen wird.

4 Conclusion

Die hier vorgestellte Faktorenanalyse sollte eingesetzt werden, wenn noch unklar ist, wie viele Faktoren in dem zu analysierenden Datensatz enthalten sind. Hat man bereits eine genaue Vorstellung von der Faktorstruktur eines Datensatzes, so sollte man statt der exploratorischen eine konfirmatorische Faktorenanalyse durchführen.

Source

Luhmann, M. (2011). R für Einsteiger.