library(tidyverse)
library(psych)
library(rockchalk)
library(bda)

affairs <- read_csv("Affairs.csv")

Table of Content

1 Introduction
2 Categorical predictors
3 Moderated regression
4 Mediation
5 Non-linear regression
6 Analysis of covariance (ANCOVA)
7 Logistic regression
8 Conclusion

1 Introduction

Aufbauend auf den Post “Regression Analysis” soll im Nachfolgenden spezielle Regressionsmodelle vorgestellt werden.

Für diesen Beitrag wurde der Datensatz Affairs von der Statistik Plattform “Kaggle” verwendet. Eine Kopie des Datensatzes ist unter https://drive.google.com/open?id=1N4osROEo724c7OZA2ARiwEthcZDwLxtf abrufbar.

2 Categorical predictors

Mit dem allgemeinen linearen Modell lassen sich sowohl kontinuierliche Prädiktoren (wie bei der einfachen Regressionsanalyse) als auch kategoriale Prädiktoren (wie bei der Varianzanalyse) analysieren. Der lm Befehl ändert sich dadurch nicht. R erkennt automatisch, dass es sich im nachfolgenden Fall bei der Prädiktorvariable um einen Faktor handelt. Für dieses Beispiel wird die Variable religiousness entsprechend umkodiert.

affairs$religiousness.r <- recode(affairs$religiousness, `1`="Gruppe 1", `2`="Gruppe 2", `3`="Gruppe 3", `4`="Gruppe 4", `5`="Gruppe 5")

Nun erfolgt die lm Syntax wie gewohnt. Es soll untersucht werden, ob es Altersunterschiede zwischen den verschiedenen Gruppen gibt.

lm.kat <- lm(affairs$age ~ affairs$religiousness.r)
summary(lm.kat)

## 
## Call:
## lm(formula = affairs$age ~ affairs$religiousness.r)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -19.221  -6.687  -1.687   5.926  26.562 
## 
## Coefficients:
##                                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                      30.4375     1.3143  23.158  < 2e-16 ***
## affairs$religiousness.rGruppe 2   0.5655     1.4943   0.378 0.705225    
## affairs$religiousness.rGruppe 3   0.6361     1.5396   0.413 0.679611    
## affairs$religiousness.rGruppe 4   3.2493     1.4710   2.209 0.027561 *  
## affairs$religiousness.rGruppe 5   6.2839     1.7065   3.682 0.000252 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 9.106 on 596 degrees of freedom
## Multiple R-squared:  0.04538,    Adjusted R-squared:  0.03897 
## F-statistic: 7.083 on 4 and 596 DF,  p-value: 1.419e-05

Das durchschnittliche Alter in der Referenzgruppe “Gruppe1” beträgt 30,44 Jahre. Dieser Wert zeigt mit p < .001, dass dieser Koeffizient signifikant von Null verschieden ist. Die weiteren Koeffizienten drücken die Unterschiede zwischen den jeweiligen Gruppen und der Referenzgruppe aus. Gruppe 2 und 3 sind nicht signifikant, d.h. es gibt keine Gruppenunterschiede in den Mittelwerten. Dahingegen ist Gruppe 4 leicht und Gruppe 5 stark signifikant.

3 Moderated regression

Bei der moderierten Regression / Moderation wird überprüft, ob der Einfluss eines Prädiktors auf das Kriterium von der Ausprägung einer dritten Moderatorvariablen abhängt. Der Einfluss der Moderatorvariablen ändert also den Effekt zwischen Prädiktor und Kriterium. Dies äußert sich so, dass die Beziehung zwischen Prädiktor und Kriterium je nach Ausprägung der Moderatorvariablen unterschiedlich ausfällt. Statistisch gesprochen liegt eine Interaktion zwischen Prädiktor und Moderatorvariable vor. Bei der Moderation wird ein Regressionsmodell mit folgenden drei Faktoren gerechnet: mit dem Prädiktor, mit der Moderatorvariable und die Interaktion zwischen dem Prädiktor und der Moderatorvariable. Diese drei Faktoren wirken auf das Kriterium. Wird in diesem Modell die Interaktion signifikant, so liegt eine signifikante Moderation vor.

Für die nachfolgende Untersuchung ist es ratsam, die verwendeten Prädiktoren zu zentrieren (siehe hierzu auch Post “Change Variables in R” Punkt 4.4). Es soll untersucht werden, ob die Anzahl der Affären (affairs) vom Alter (age) und vom Bildungsstand (education) abhängig sind. Das Alter soll hierbei der Prädiktor (X) sein, die Anzahl der Affären das Kriterium (Y) und der Bildungsstand (Z) soll als Moderatorvariable dienen.

age.cen <- as.numeric(scale(affairs$age, scale = FALSE))
education.cen <- as.numeric(scale(affairs$education, scale = FALSE))
affairs.normal <- as.numeric(affairs$affairs)

lm.mod <- lm(affairs.normal ~ age.cen * education.cen)

summary(lm.mod)

## 
## Call:
## lm(formula = affairs.normal ~ age.cen * education.cen)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -2.789 -1.564 -1.258 -0.860 10.899 
## 
## Coefficients:
##                        Estimate Std. Error t value Pr(>|t|)    
## (Intercept)            1.436301   0.135077  10.633   <2e-16 ***
## age.cen                0.036177   0.014643   2.471   0.0138 *  
## education.cen         -0.038808   0.058195  -0.667   0.5051    
## age.cen:education.cen  0.006538   0.005400   1.211   0.2265    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.288 on 597 degrees of freedom
## Multiple R-squared:  0.01173,    Adjusted R-squared:  0.006768 
## F-statistic: 2.363 on 3 and 597 DF,  p-value: 0.07025

Der Haupteffekt Alter ist signifikant, d.h. die Anzahl an Affären steigt mit dem Alter, bei einem durchschnittlichen Bildungsgrad, an. Der Haupteffekt Bildungsgrad ist mit p = .505 nicht signifikant, d.h. es gibt keinen Zusammenhang zwischen Bildungsgrad und der Anzahl an Affären, wenn das Alter einen durchschnittlichen Wert aufweist. Der Interaktionseffekt ist zwar ebenfalls nicht signifikant, er wird aber für dieses Beispiel dennoch weiter untersucht. Für die Interpretation des Interaktionseffektes bieten sich bedingte Regressionsgleichungen zur Veranschaulichung an. Dabei wird die Auswirkung des Prädiktors (x) auf das Kriterium (Y) für verschiedene Ausprägungen der Moderatorvariable (Z) berechnet.

Steigung <- plotSlopes(lm.mod, plotx = "age.cen", modx = "education.cen")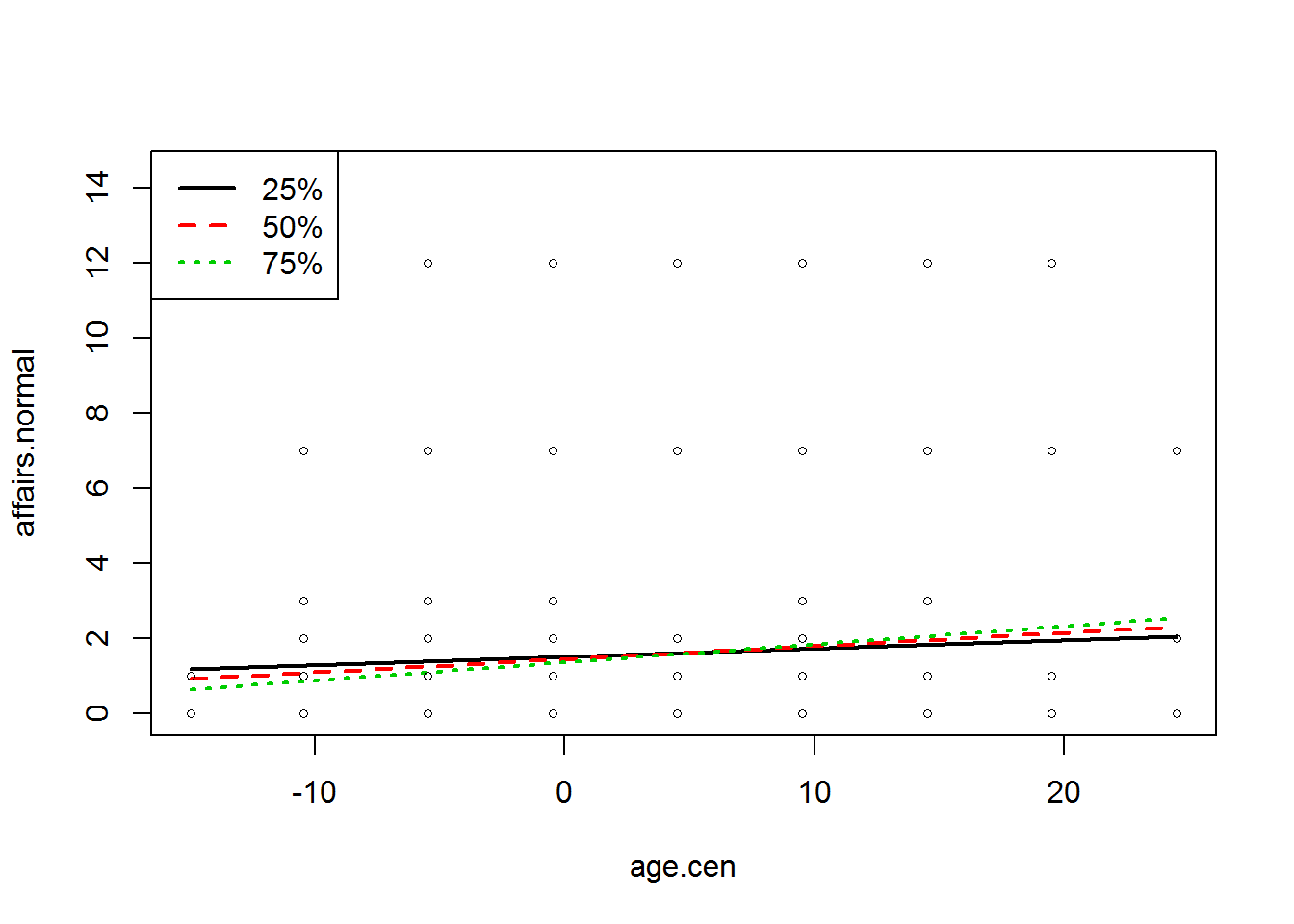

Zu Beginn der plotSlopes Funktion wird der Name des Regressionsmodells genannt. plotx = “” beinhaltet den Namen der Variable X und modx =“” den Namen der Variablen Z (für die die bedingte Regressionsgleichung erstellt werden sollen).

Es werden drei bedingte Regressionsgleichung, für die Quartile der Moderatorvariablen, in der Abbildung dargestellt.

Das Objekt “Steigung” enthält folgende Werte.

Steigung

## $call
## plotSlopes.lm(model = lm.mod, plotx = "age.cen", modx = "education.cen")
## 
## $newdata
##     age.cen education.cen       fit
## 1 -14.98752    -2.1663894 1.1904443
## 2 -14.98752    -0.1663894 0.9168548
## 3 -14.98752     1.8336106 0.6432654
## 4  24.51248    -2.1663894 2.0599861
## 5  24.51248    -0.1663894 2.3028881
## 6  24.51248     1.8336106 2.5457901
## 
## $modxVals
##        25%        50%        75% 
## -2.1663894 -0.1663894  1.8336106 
## 
## $col
## 25% 50% 75% 
##   1   2   3 
## 
## $lty
## 25% 50% 75% 
##   1   2   3 
## 
## attr(,"class")
## [1] "plotSlopes" "rockchalk"

Die $modxVals Angabe enthält die Werte der Moderatorvariablen, die für die Berechnung der bedingten Regressionsgleichungen eingesetzt wurden.

Nun soll untersucht werden, unter welchen Umständen sich die bedingten Regressionsgewichte signifikant von Null unterscheiden. Dies kann mittels der testSlopes Funktion berechnet werden.

testSlopes(Steigung)

## Values of education.cen INSIDE this interval:
##         lo         hi 
## -0.9901723  6.9786332 
## cause the slope of (b1 + b2*education.cen)age.cen to be statistically significant

Das Regressionsgewicht ist signifikant von Null verschieden, wenn der Wert der Moderatorvariablen kleiner als -0,99 oder größer als 6,98 ist.

4 Mediation

Entgegengesetzt zur Moderation steht bei der Mediation die Mediatorvariable in Beziehung sowohl zu dem Prädiktor als auch zum Kriterium. Der direkte Effekt zwischen Prädiktor und Kriterium wird durch den indirekten Effekt über die Mediatorvariable erklärt. Es werden erneut mehrere Regressionsmodelle gerechnet. Wenn folgende Bedingungen erfüllt sind, liegt eine signifikante Mediation vor:

im ersten Modell (Prädiktor -> Kriterium) ist der Regressionskoeffizient von dem Prädiktor signifikant,
im zweiten Modell (Prädiktor -> Mediatorvariable) ist der Regressionskoeffizient von dem Prädiktor signifikant,
im dritten Modell (Prädiktor und Mediatorvariable -> Kriterium) ist der Regressionskoeffizient von der Mediatorvariable signifikant und
im dritten Modell ist der Regressionskoeffizient von dem Prädiktor kleiner als im ersten Modell.

Nachfolgend soll untersucht werden, ob die Anzahl der Affären (affairs) vom Alter (age) und vom Bildungsstand (education) abhängig sind. Das Alter soll hierbei der Prädiktor (X) sein, die Anzahl der Affären das Kriterium (Y) und der Bildungsstand (Z) soll als Mediatorvariable dienen. Eine Mediation kann folgender maßen berechnet werden.

affairs$age.cen <- as.numeric(scale(affairs$age, scale = FALSE))
affairs$education.cen <- as.numeric(scale(affairs$education, scale = FALSE))
affairs$affairs.normal <- as.numeric(affairs$affairs)


m.mod <- mediate(affairs.normal ~ age.cen + (education.cen), data = affairs)
mediate(y = affairs.normal ~ age.cen + (education.cen), data = affairs)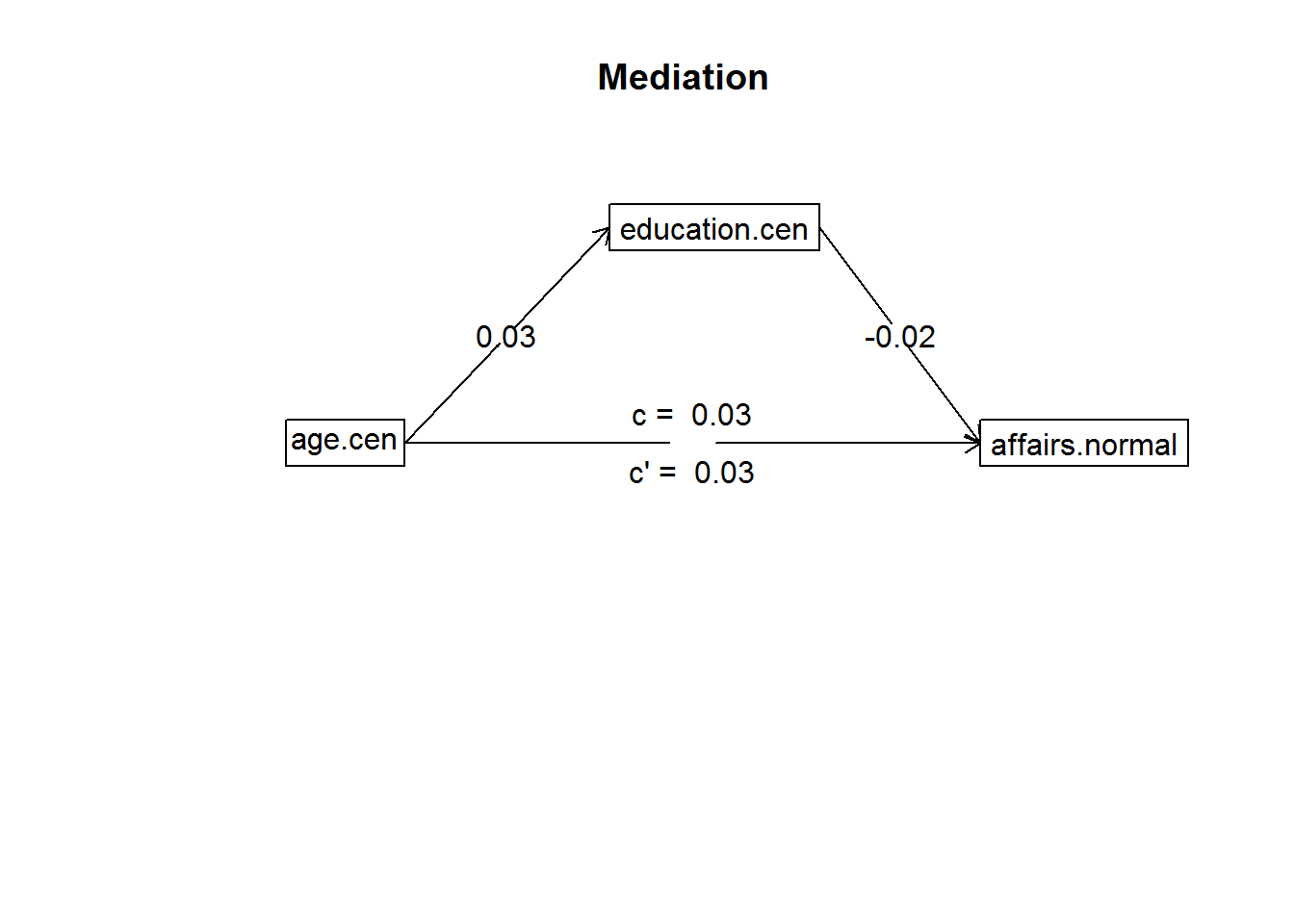

## 
## Mediation/Moderation Analysis 
## Call: mediate(y = affairs.normal ~ age.cen + (education.cen), data = affairs)
## 
## The DV (Y) was  affairs.normal . The IV (X) was  age.cen . The mediating variable(s) =  education.cen .
## 
## Total effect(c) of  age.cen  on  affairs.normal  =  0.03   S.E. =  0.01  t  =  2.34  df=  598   with p =  0.02
## Direct effect (c') of  age.cen  on  affairs.normal  removing  education.cen  =  0.03   S.E. =  0.01  t  =  2.37  df=  598   with p =  0.018
## Indirect effect (ab) of  age.cen  on  affairs.normal  through  education.cen   =  0 
## Mean bootstrapped indirect effect =  0  with standard error =  0  Lower CI =  -0.01    Upper CI =  0
## R = 0.1 R2 = 0.01   F = 2.81 on 2 and 598 DF   p-value:  0.0611 
## 
##  To see the longer output, specify short = FALSE in the print statement or ask for the summary

summary(m.mod)

## Call: mediate(y = affairs.normal ~ age.cen + (education.cen), data = affairs)
## 
##  Total effect estimates (c) 
##         affairs.normal   se    t  df   Prob
## age.cen           0.03 0.01 2.34 598 0.0195
## 
## Direct effect estimates     (c') 
##               affairs.normal   se     t  df   Prob
## age.cen                 0.03 0.01  2.37 598 0.0181
## education.cen          -0.02 0.06 -0.38 598 0.7050
## 
## R = 0.1 R2 = 0.01   F = 2.81 on 2 and 598 DF   p-value:  0.0611 
## 
##  'a'  effect estimates 
##         education.cen   se    t  df    Prob
## age.cen          0.03 0.01 3.32 599 0.00094
## 
##  'b'  effect estimates 
##               affairs.normal   se     t  df  Prob
## education.cen          -0.02 0.06 -0.38 598 0.705
## 
##  'ab'  effect estimates 
##         affairs.normal boot sd lower upper
## age.cen              0    0  0 -0.01     0

Ergebnisse:

age -> education: b = 0,03, se = 0,01, p = .001
education -> affairs: b = -0,02, se = 0,06, p = .705
Totaler Effekt age -> affairs: b = 0,03, se = 0,01, p = .02
Direkter Effekt age -> affairs: b = 0,03, se = 0,01, p = .018
Indirekter Effekt age -> affairs: b = 0, 95% KI = [-0,01 - 0]

Der Sobel Test überprüft anschließend noch den indirekten Effekt auf Signifikanz. Wichtig bei der mediation.test() Funktion ist die Reihenfolge: Mediatorvariable, Prädiktor, Kriterium.

mediation.test(affairs$education.cen, affairs$age.cen, affairs$affairs.normal)

##              Sobel     Aroian    Goodman
## z.value -0.3758358 -0.3600966 -0.3938373
## p.value  0.7070390  0.7187749  0.6937011

Mit p = .707 liegt keine signifikante Mediation vor.

5 Non-linear regression

Bei nicht linearen Regressionen soll untersucht werden, ob die Auswirkung einer Variablen X auf das Kriterium Y ab einen gewissen Grad stärker zunimmt, abnimmt oder sich sogar in die entgegengesetzte Richtung umschwenkt. Beispielhaft kann man hier Untersuchungen zum Kaffeekonsum erwähnen. Kaffee (beziehungsweise das Koffein) bewirkt zum Anfang eine positive Auswirkung auf die Konzentration. Ab einer bestimmten Menge an Kaffee flacht die Auswirkungen auf die Konzentrationsfähigkeit ab und bewirkt bei weiterer Zuführung von Koffein sogar eine Beeinträchtigung der Konzentration.

Nicht lineare Zusammenhänge können in der Regressionsanalyse modelliert werden, wenn Polynome höherer Ordnung in die Gleichung aufgenommen werden.

Es soll untersucht werden, ob die Anzahl an verheirateten Jahren, einen nicht linearen Zusammenhang zu der Anzahl an Affären aufweisen. Dafür ist es wieder notwendig, die zu untersuchenden Variablen zu zentrieren (die Variable affairs wurde bereits zentriert und unter dem Objekt “affairs.normal” abgespeichert).

years.married.cen <- as.numeric(scale(affairs$yearsmarried, scale = FALSE))

Anschließend wird das nicht lineare Modell spezifiziert, indem die years.married Variable zweimal aufgnommen wird.

lm.nlm <- lm(affairs.normal ~ years.married.cen + I(years.married.cen^2))
summary(lm.nlm)

## 
## Call:
## lm(formula = affairs.normal ~ years.married.cen + I(years.married.cen^2))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.1033 -1.9001 -1.0936 -0.3194 11.5994 
## 
## Coefficients:
##                         Estimate Std. Error t value Pr(>|t|)    
## (Intercept)             1.720059   0.241827   7.113 3.26e-12 ***
## years.married.cen       0.114330   0.023921   4.779 2.22e-06 ***
## I(years.married.cen^2) -0.008524   0.006534  -1.305    0.193    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.241 on 598 degrees of freedom
## Multiple R-squared:  0.03765,    Adjusted R-squared:  0.03443 
## F-statistic:  11.7 on 2 and 598 DF,  p-value: 1.039e-05

Nur ein Regressionsgewicht der Prädiktoren ist signifikant von Null verschieden, d.h. es liegt kein kurvilinearer Zusammenhang vor. Dafür müssten beide Regressionsgewichtet sich signifikant von Null unterscheiden. Wäre dies der Fall, so könnte man für eine vereinfachte Interpretation folgende Grafik (Streudiagramm) erstellen.

plot(years.married.cen, affairs.normal, xlab = "Anzahl verheirateter Jahre zentriert", ylab = "Affären vs. Treue")
curve(1.720059 + 0.114330*x - 0.008524*(x^2), add=TRUE)
abline(lm(affairs.normal ~ years.married.cen))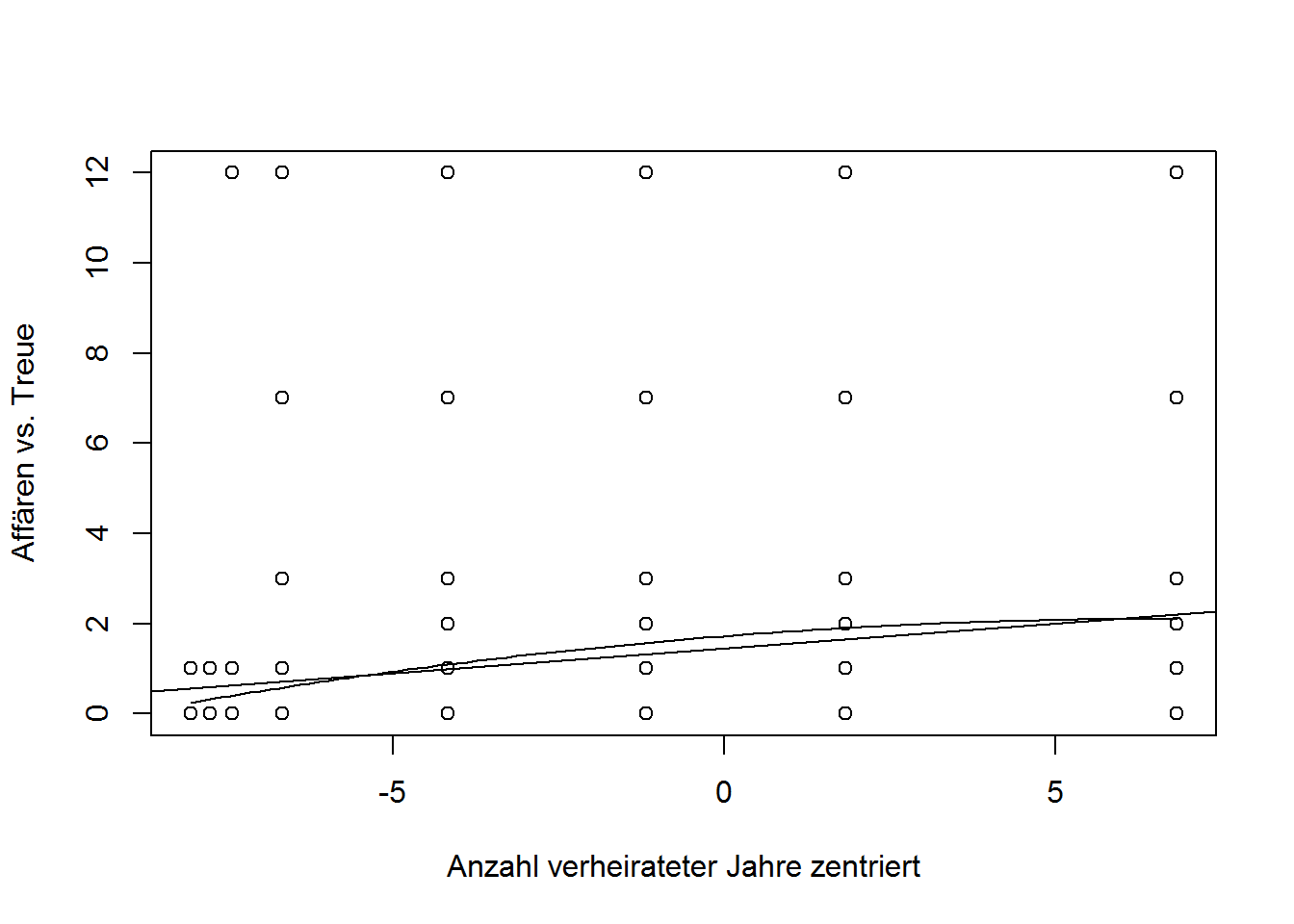

6 Analysis of covariance (ANCOVA)

Die Kovarianzanalyse erlaubt die Kombination von kategorialen und metrischen Prädiktoren in einem einzigen linearen Modell. Im Nachfolgenden soll der Einfluss des Alters (zentriert) und des Geschlechts auf die Anzahl an Affären untersucht werden.

sex <- affairs$gender
table(sex)

## sex
## female   male 
##    315    286

Merke: “female” wird an erster Stelle genannt.

cov <- lm(affairs.normal ~ age.cen * sex)
summary(cov)

## 
## Call:
## lm(formula = affairs.normal ~ age.cen * sex)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -2.511 -1.570 -1.261 -1.030 11.135 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      1.48930    0.18895   7.882 1.53e-14 ***
## age.cen          0.04167    0.02148   1.940   0.0529 .  
## sexmale         -0.04423    0.27385  -0.162   0.8717    
## age.cen:sexmale -0.01397    0.02952  -0.473   0.6362    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.291 on 597 degrees of freedom
## Multiple R-squared:  0.009485,   Adjusted R-squared:  0.004507 
## F-statistic: 1.906 on 3 and 597 DF,  p-value: 0.1275

Der vorhergesagt Wert (Intercept) für Frauen (wg erster Stelle der table(sex) Funktion) beträgt 1,49 bei durchschnittlichem Alter. Der Koeffizient age.cen beschreibt den Zusammenhang zwischen Alter und der Anzahl an Affären für Frauen. Der Koeffizient sexmale drückt hier den Unterschied zwischen Männer und Frauen hinsichtlich der Anzahl an Affären bei durchschnittlichem Lebensalter aus. Der Interaktionseffekt (age.cen:sexmale) beschreibt das Ausmaß, in dem sich die Stärke des Zusammenhangs zwischen Alter und Anzahl an Affären für Männer von den Frauen unterscheidet. In dem vorangegangenen Beispiel sind weder die Haupteffekte noch der Interaktionseffekt statistisch signifikant. Wäre der Interaktionseffekt signifikant gewesen, so würde sich zur besseren Interpretation (wie bei der moderierten Regression) die Berechnung und die graphische Darstellung der bedingten Regressionsgleichungen anbieten.

Steigung2 <- plotSlopes(cov, plotx = "age.cen", modx = "sex")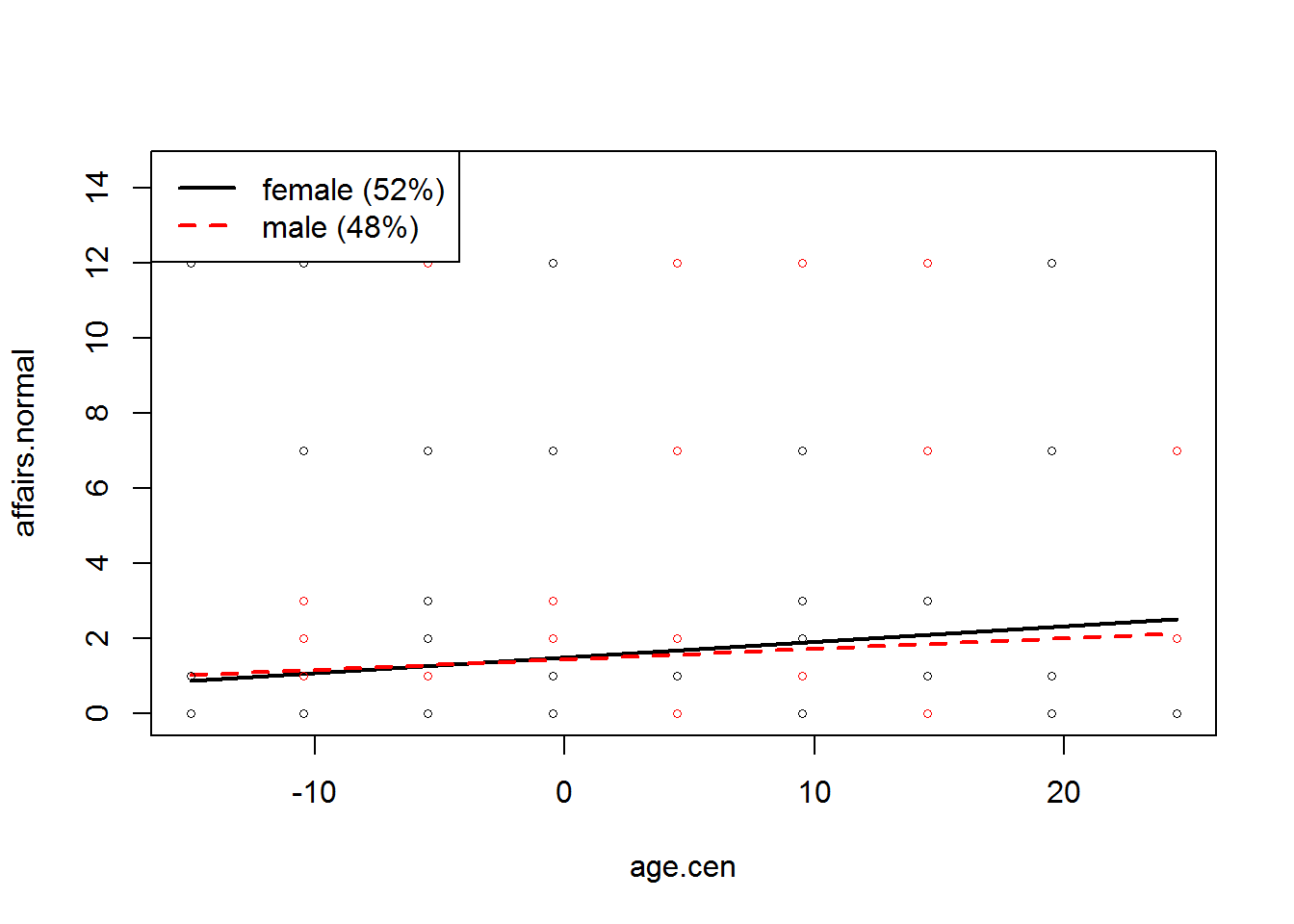

Anschließend wird noch ein Signifikanztest für die beiden Regressionsgewichte durchgeführt.

testSlopes(Steigung2)

## These are the straight-line "simple slopes" of the variable age.cen  
##  for the selected moderator values. 
##             "sex"      slope Std. Error  t value   Pr(>|t|)
## 1         age.cen 0.04167150 0.02148213 1.939822 0.05287201
## 2 age.cen:sexmale 0.02769793 0.02025154 1.367695 0.17192212

Dieser Ausgabe kann entnommen werden, dass weder das Lebensalter bei Frauen (p = .053) noch das bei Männern (p= .172) signifikant mit der Anzahl an Affären zusammenhängt.

7 Logistic regression

Die bisherig vorgestellten speziellen Regressionsmodelle hatten die Gemeinsamkeit, dass das untersuchte Kriterium metrisch war. Mit der logistischen Regression ist es möglich, eine kategoriale abhängige Variable zu analysieren. Diese muss auch nicht zwingend dichotom sein, sondern kann auch mehr als zwei Ausprägungen besitzen.

Im folgenden Beispiel soll der Unterschied zwischen Männer und Frauen Frauen hinsichtlich des Bildungsgrades untersucht werden. Das Geschlecht ist hierbei das Kriterium. Für die logistische Regression ist es wichtig, dass die erste Kategorie mit 0 und die zweite Kategorie mit 1 kodiert ist.

affairs$gender.r <- recode(affairs$gender, `male`="0", `female`="1")
sex.r <- as.numeric(affairs$gender.r)

Im zweiten Schritt wird die unabhängige Variable einem Objekt zugeordnet.

education.normal <- as.numeric(affairs$education)

Modelle mit nicht-metrischen abhängigen Variablen werden als Generalized Linear Models (Generalisierte Lineare Modelle) bezeichnet und können in R mit der glm Funktion berechnet werden. Im nachfolgenden Beispiel wird eine lineare Regression mit der abhängigen Variable sex.r und der unabhängigen Variable education.normal angefordert.

log.lm <- glm(sex.r ~ education.normal, family = binomial)

Auch bei dem glm Befehl funktioniert die summary Funktion.

summary(log.lm)

## 
## Call:
## glm(formula = sex.r ~ education.normal, family = binomial)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.4333  -0.9405   0.5680   1.0980   1.7838  
## 
## Coefficients:
##                  Estimate Std. Error z value Pr(>|z|)    
## (Intercept)       6.40144    0.70153   9.125   <2e-16 ***
## education.normal -0.38823    0.04266  -9.100   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 831.76  on 600  degrees of freedom
## Residual deviance: 729.05  on 599  degrees of freedom
## AIC: 733.05
## 
## Number of Fisher Scoring iterations: 4

Für den Prädiktor education.normal erhalten wir den Regressionskoeffizienten b₁=-0,39, z=-9,1, p<.001. Der Bildungsgrad ist also ein signifikanter Prädiktor für die Variable sex.r. Zur genaueren Interpretation dieses Koeffizienten wird daran erinnert, dass die zweite Kategorie (female) mit 1 kodiert worden ist. Der Regressionskoeffizient wird daher wie folgt interpretiert: Wenn man den Bildungsgrad um eine Einheit erhöht, reduziert sich der Logit um -0,39. Der Logit ist der natürliche Logarithmus des Wettquotienten. Der Achsenabschnitt (Intercept, hier 6,40) drückt die Höhe des Logits für einen Bildungsgrad von Null aus. Des Weiteren erhalten wir mit der summary Funktion bei glm Modellen Angaben zu den Devianzen. Diese sind ein Maß für die Modellgüte. Je kleiner die Devianz ist, desto besser passt das Modell auf die Daten. Die Zeile Null deviance enthält die Devianz des Nullmodells (ein Modell, das keien Prädiktoren enthält). Die Zeile Residual deviance ist die Devianz für das von uns durchgeführte Modell. Diese Devianz sollte deutlich kleiner sein als die von dem Nullmodell. Die Angabe AIC steht für Akaikes Information Criterion und ist ebenfalls ein Indikator für die Modellgüte. Je kleiner der AIC ausfällt, desto besser ist das Modell. Die Ausgabe Number of Fisher Scoring iterations: 4 zeigt an, wie viele Iterationen benötigt wurden, um die Modellparameter zu schätzen. Eine hohe Anzahl (> 25) würde darauf hindeute, dass das Modell nicht gut auf die Daten passt.

Zusätzlich zu den Regressionskoeffizienten wird das Odds Ratio berechnet. Dies dient auch als Effektgröße für die einzelnen Koeffizienten. Als erstes werden nochmals die Regressionskoeffizienten des “log.lm” Objektes angefordert.

coef(log.lm)

##      (Intercept) education.normal 
##        6.4014447       -0.3882297

Das Odds Ratio lässt sich aus den Koeffizienten berechnen, indem man diese exponiert.

exp(coef(log.lm))

##      (Intercept) education.normal 
##      602.7151603        0.6782565

Zusätzlich können Konfidenzintervalle für das Odds Ratio angefordert werden.

exp(confint(log.lm))

## Waiting for profiling to be done...

##                      2.5 %       97.5 %
## (Intercept)      157.82480 2476.8976498
## education.normal   0.62243    0.7358748

Ähnlich wie bei der multiplen linearen Regression kann auch bei der logistischen Regression verschiedene Modelle miteinander verglichen werden (hierarchisches Vorgehen). Im ersten Modell wurde der Unterschied zwischen Männer und Frauen hinsichtlich des Bildungsgrades untersucht (hier nochmal neu abgespeichert unter dem Objekt “log.lm1”).

log.lm1 <- glm(sex.r ~ education.normal, family = binomial)

In einem weiteren Modell soll der Unterschied zwischen Männer und Frauen hinsichtlich des Bildungsgrades und der Religiosität untersucht werden.

reli <- as.numeric(affairs$religiousness)
log.lm2 <- glm(sex.r ~ education.normal + reli, family = binomial)
summary(log.lm2)

## 
## Call:
## glm(formula = sex.r ~ education.normal + reli, family = binomial)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.4196  -0.9781   0.5532   1.0765   1.8053  
## 
## Coefficients:
##                  Estimate Std. Error z value Pr(>|z|)    
## (Intercept)       6.56873    0.75431   8.708   <2e-16 ***
## education.normal -0.38943    0.04276  -9.107   <2e-16 ***
## reli             -0.04789    0.07698  -0.622    0.534    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 831.76  on 600  degrees of freedom
## Residual deviance: 728.66  on 598  degrees of freedom
## AIC: 734.66
## 
## Number of Fisher Scoring iterations: 4

Der zusätzliche Prädiktor reli ist nicht signifikant (b₂=-0,05, z=-,62, p=.534).

Nun werden die beiden Modelle auf Signifikanz getestet.

anova(log.lm1, log.lm2, test = "Chi")

## Analysis of Deviance Table
## 
## Model 1: sex.r ~ education.normal
## Model 2: sex.r ~ education.normal + reli
##   Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1       599     729.05                     
## 2       598     728.66  1  0.38756   0.5336

Die Resid. Df Spalte enthält die Freiheitsgrade und die Resid. Dev Spalte die Residualdevianzen der beiden Modellgleichungen. Die Residualdevianz des zweiten Modells (D₂ = 728,66) fällt etwas kleiner aus als die Residualdevianz des ersten Modells (D₁ = 729,05). Das zweite Modell passt demnach etwas besser auf die Daten. Diese Verbesserung muss aber noch auf Signifikanz überprüft werden. Die Spalte Deviance enthält den Chi^2-Wert (die Differenz der beiden Devianzen) und die dazugehörigen Freiheitsgrade für den Test sind unter der Spalte Df aufgeführt. Diese entsprechen der Differenz der Freiheitsgrade der beiden Modelle, hier also 599-598 = 1 Freiheitsgrad. Der durchgeführte Chi^2-Test ist mit chi^2=0,39, df=1, p=.534 nicht signifikant. Dies bedeutet, dass das zweite Modell nicht signifikant besser auf die Daten passt als das sparsamere Modell. Es wird daher das Modell 1 (log.lm1) bevorzugt.

8 Conclusion

Ergänzend zu dem Post “Regression Analysis” wurde in diesem Beitrag die Aufnahme von kategorialen Prädiktoren (Punkt 2) in lineare Regressionsmodelle behandelt. Des Weiteren wurde gezeigt, wie eine Moderation (Punkt 3) und eine Mediation (Punkt 4) durchgeführt und interpretiert werden kann. Die Modellierung nicht-linearer Zusammenhänge wurde unter Punkt 5 thematisiert. Zum Schluss war die Kovarianzanalyse (Punkt 6) und die logistische Regression (Punkt 7), bei der eine dichotome abhängige Variable vorlag, zentral.

Source

Luhmann, M. (2011). R für Einsteiger.

Special Regression Analysis