Table of Content

1 Introduction
2 purrr::map() function
3 How to request with map() some statistical values
4 How to use map() for multiple t-tests
5 How to use map() for multiple linear regressions
6 Conclusion

library(tidyverse)
library(purrr)
library(broom)
library(knitr)
library(psych)

affairs <- read_csv("Affairs.csv")

1 Introduction

Sehr häufig werden R-Befehle per Copy & Paste vervielfacht und anschließend für unterschiedliche Zwecke leicht abgewandelt. Dies ist nicht nur umständlich, sondern auch leicht fehleranfällig. Vor diesem Hintergrund werden im Nachfolgenden Möglichkeiten aufgezeigt, wie man effektive Codes in R schreiben kann, ohne einen Befehl doppelt zu verwenden.

Für diesen Post wurde der Datensatz Affairs von der Statistik Plattform “Kaggle” verwendet. Eine Kopie des Datensatzes ist unter https://drive.google.com/open?id=1N4osROEo724c7OZA2ARiwEthcZDwLxtf abrufbar.

2 purrr::map() function

Als kurze Einführung wird die Frage beantwortet, was die map Funktion aus dem purrr Package macht.

v <- list(1, 2, 3)
map(v, ~ .* 10)

## [[1]]
## [1] 10
## 
## [[2]]
## [1] 20
## 
## [[3]]
## [1] 30

Die map Funktion transformiert einen Input durch die Anwendung einer Funktion auf jedes Element des Inputs und gibt anschließend einen Vektor aus, der dieselbe Länge besitzt wie die des Inputs. In unserem Beispiel wurde R der Befehl gegeben, jedes Element aus v (zuvor erstelltes Objekt) mit 10 zu multiplizieren.

3 How to request with map() some statistical values

glimpse(affairs)

## Observations: 601
## Variables: 10
## $ X1            <int> 4, 5, 11, 16, 23, 29, 44, 45, 47, 49, 50, 55, 64...
## $ affairs       <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...
## $ gender        <chr> "male", "female", "female", "male", "male", "fem...
## $ age           <dbl> 37, 27, 32, 57, 22, 32, 22, 57, 32, 22, 37, 27, ...
## $ yearsmarried  <dbl> 10.00, 4.00, 15.00, 15.00, 0.75, 1.50, 0.75, 15....
## $ children      <chr> "no", "no", "yes", "yes", "no", "no", "no", "yes...
## $ religiousness <int> 3, 4, 1, 5, 2, 2, 2, 2, 4, 4, 2, 4, 5, 2, 4, 1, ...
## $ education     <int> 18, 14, 12, 18, 17, 17, 12, 14, 16, 14, 20, 18, ...
## $ occupation    <int> 7, 6, 1, 6, 6, 5, 1, 4, 1, 4, 7, 6, 6, 5, 5, 5, ...
## $ rating        <int> 4, 4, 4, 5, 3, 5, 3, 4, 2, 5, 2, 4, 4, 4, 4, 5, ...

Für die Beschreibung eines Datensatzes werden häufig sehr viele statistische Kennzahlen (Median, Mittelwert, Standardabweichung, …) angefordert. Dies jeweils mit einem eigenen Befehl zu tun ist besonders bei großen Datensätzen mit vielen Variablen sehr zeitintensiv und auch völlig überflüssig, denn hierfür kann prima auch die map Funktion verwendet werden.

Zu Beginn einer Analyse ist meist von Interesse, ob und wenn ja wie viele fehlende Werte im Datensatz vorhanden sind. Dies kann folgendermaßen überprüft werden.

affairs %>% 
  map(~sum(is.na(.)))

## $X1
## [1] 0
## 
## $affairs
## [1] 0
## 
## $gender
## [1] 0
## 
## $age
## [1] 0
## 
## $yearsmarried
## [1] 0
## 
## $children
## [1] 0
## 
## $religiousness
## [1] 0
## 
## $education
## [1] 0
## 
## $occupation
## [1] 0
## 
## $rating
## [1] 0

Man sieht, dass bei keiner Variablen des Datensatzes “affairs” ein fehlender Wert (NA) existiert. Dieselbe Überprüfung kann auch pro Zeile erfolgen. Aus Übersichtsgründen wurde die Ausgabe des Befehls hier unterdrückt.

apply(affairs,MARGIN = 1, FUN = function(x) sum(is.na(x)))

Mit dem select Befehl können auch gezielt Spalten ausgewählt werden, für die anschließend mit der map Funktion die Kennzahlen angefordert werden sollen.

affairs %>% select(7:10) %>% map(describeBy)

## $religiousness
##    vars   n mean   sd median trimmed  mad min max range  skew kurtosis
## X1    1 601 3.12 1.17      3    3.12 1.48   1   5     4 -0.09    -1.02
##      se
## X1 0.05
## 
## $education
##    vars   n  mean  sd median trimmed  mad min max range  skew kurtosis  se
## X1    1 601 16.17 2.4     16   16.21 2.97   9  20    11 -0.25    -0.32 0.1
## 
## $occupation
##    vars   n mean   sd median trimmed  mad min max range  skew kurtosis
## X1    1 601 4.19 1.82      5    4.34 1.48   1   7     6 -0.74    -0.79
##      se
## X1 0.07
## 
## $rating
##    vars   n mean  sd median trimmed  mad min max range  skew kurtosis   se
## X1    1 601 3.93 1.1      4    4.07 1.48   1   5     4 -0.83    -0.22 0.04

Meistens sind jedoch nur gezielte Kennzahlen von bestimmten Variablen von Interesse. Der Datensatz Affairs wird deshalb auf folgende 5 Variablen beschränkt.

affairs.short <- affairs %>% select(age, 7:10)
affairs.short

## # A tibble: 601 x 5
##      age religiousness education occupation rating
##    <dbl>         <int>     <int>      <int>  <int>
##  1    37             3        18          7      4
##  2    27             4        14          6      4
##  3    32             1        12          1      4
##  4    57             5        18          6      5
##  5    22             2        17          6      3
##  6    32             2        17          5      5
##  7    22             2        12          1      3
##  8    57             2        14          4      4
##  9    32             4        16          1      2
## 10    22             4        14          4      5
## # ... with 591 more rows

Es soll nun der Mittelwert für alle 5 Variablen angefordert werden. Dafür würde sich die for loop Funktion anbieten.

output <- vector("double", length(affairs.short))
            for (i in seq_along(affairs.short)) {
              output[[i]] <- mean(affairs.short[[i]])
            }
output

## [1] 32.487521  3.116473 16.166389  4.194676  3.931780

Man könnte dies auch gleich als Funktion schreiben.

col_mean <- function(df) {
  output <- vector("double", length(df))
  for (i in seq_along(df)) {
    output[i] <- mean(df[[i]])
  }
  output
}


col_mean(affairs.short)

## [1] 32.487521  3.116473 16.166389  4.194676  3.931780

Man sieht, dass die Funktion klappt. Leicht abgewandelt, kann diese auch andere statistische Kennwerte berechnen. Im Nachfolgenden werden die Befehle auf die gleiche Art und Weise für die Standardabweichung und den Median erstellt.

col_sd <- function(df) {
  output <- vector("double", length(df))
  for (i in seq_along(df)) {
    output[i] <- sd(df[[i]])
  }
  output
}



col_median <- function(df) {
  output <- vector("double", length(df))
  for (i in seq_along(df)) {
    output[i] <- median(df[[i]])
  }
  output
}

Anschließend erfolgt eine gemeinsame Ausgabe der statistischen Werte.

col_mean(affairs.short)

## [1] 32.487521  3.116473 16.166389  4.194676  3.931780

col_sd(affairs.short)

## [1] 9.288762 1.167509 2.402555 1.819443 1.103179

col_median(affairs.short)

## [1] 32  3 16  5  4

Auch dies funktioniert wie erwartet. Für eine bessere Übersicht, können die Zeilen miteinander verbunden werden.

Mittelwert<-col_mean(affairs.short)
Median<-col_median(affairs.short)
standardabweichung<-col_sd(affairs.short)
cbind(Mittelwert,Median ,standardabweichung)

##      Mittelwert Median standardabweichung
## [1,]  32.487521     32           9.288762
## [2,]   3.116473      3           1.167509
## [3,]  16.166389     16           2.402555
## [4,]   4.194676      5           1.819443
## [5,]   3.931780      4           1.103179

An und für sich ein zufriedenstellendes Ergebnis. Jedoch wurde wieder ein Fehler gemacht, der in diesem Post eigentlich vermieden werden sollte. Es wurde erneut copy & paste angewendet.

Die zentrale Frage ist: wie können die drei Funktionen in einer Syntax miteinander verbunden werden?

Zur Beantwortug dieser Frage werden beispielhaft folgende drei Funktionen erstellt.

fun1 <- function(x) abs(x - mean(x))^1
fun2 <- function(x) abs(x - mean(x))^2
fun3 <- function(x) abs(x - mean(x))^3

Diese in einer Syntax zu schreiben könnte folgendermaßen aussehen:

fun.ges <- function(x, i) abs(x - mean(x))^i

Genau dieses Prinzip lässt sich auch auf die Funktionen der statistischen Kennwerte anwenden.

col_summary <- function(df, fun) {
  out <- vector("double", length(df))
  for (i in seq_along(df)) {
    out[[i]] <- fun(df[[i]])
  }
  out
}

Die erstellte col_summary Funktion lässt sich nun beliebig auf jeden Datensatz (Argument 1) und R-Befehl (Argument 2) anwenden. Hier die Anforderung des Medians für die Variablen im Datensatz “affairs.short”

col_summary(affairs.short, median)

## [1] 32  3 16  5  4

Man sieht das gleiche Ergebnis wie bei der zuvor erstellten “Einzelfunkton” für den Median (col_median(affairs.short)).

4 How to use map() for multiple t-tests

Mit map lässt sich ein kompletter Datensatz auch sehr schnell und effizient auf beispielsweise Geschlechterunterschiede mittels t-tests untersuchen.

affairs %>% select(age, affairs, yearsmarried, education, religiousness) %>% 
  map(function(x) t.test(x ~ affairs$gender)$p.value)

## $age
## [1] 2.848452e-06
## 
## $affairs
## [1] 0.7739606
## 
## $yearsmarried
## [1] 0.458246
## 
## $education
## [1] 9.772643e-24
## 
## $religiousness
## [1] 0.8513998

Männer und Frauen unterscheiden sich also signifikant in dieser Stichprobe nur in ihrem Alter und der Ausbildung.

affairs %>% select(age, affairs, yearsmarried, education, religiousness) %>% map(function(x) t.test(x ~ affairs$gender)$p.value) %>%
  as.data.frame %>% gather %>% mutate(signif = ifelse(value < .05, "significant", "n.significant")) %>%
  ggplot(aes(x = reorder(key, value), y = value)) + 
  geom_point(aes(color=signif)) + 
  coord_flip() +
  ylab("p-value")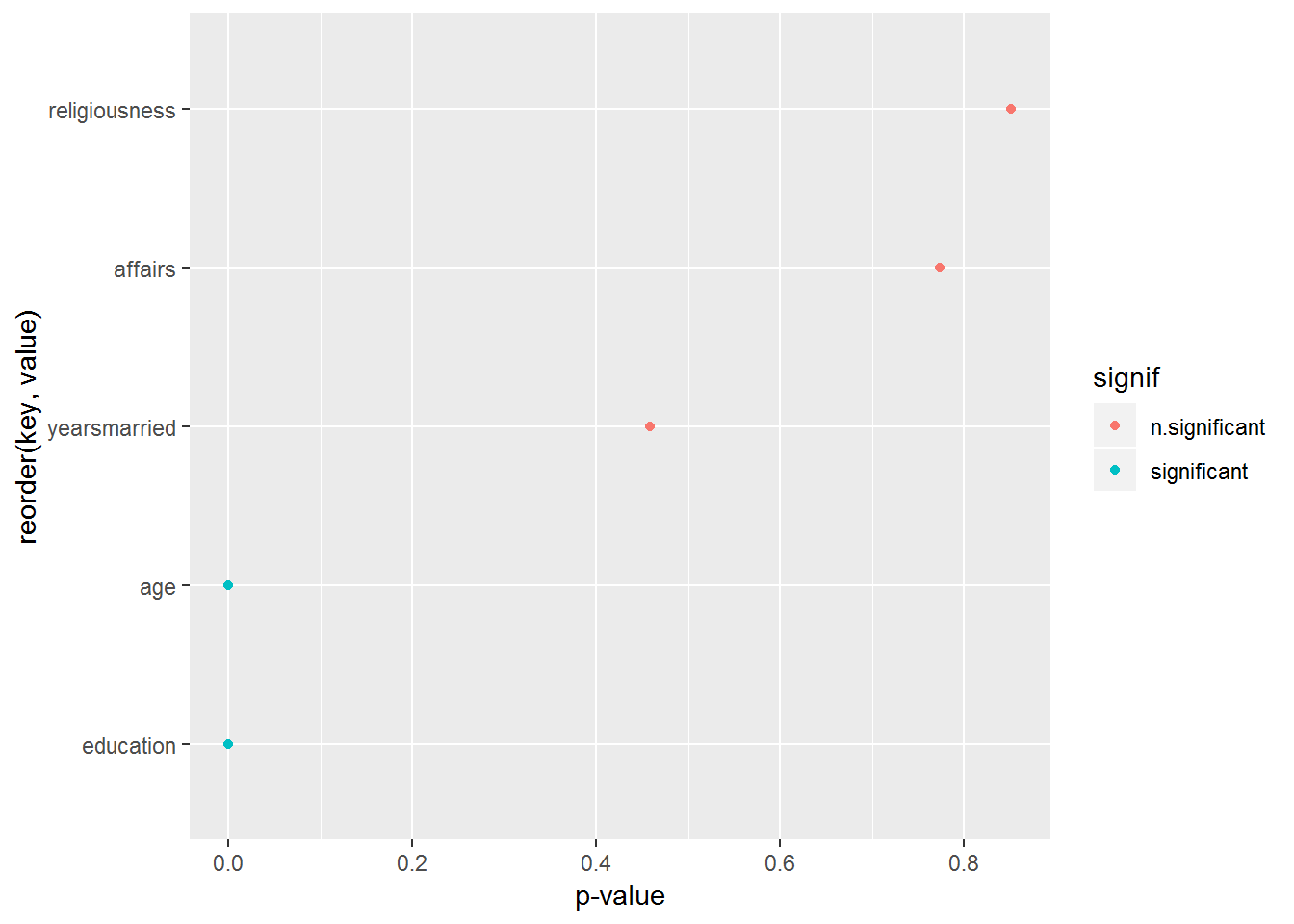

5 How to use map() for multiple linear regressions

Was mit dem t-Test ging, geht auch für die einfache lineare Regression. Hierbei wird aber nicht der p-Wert angefordert, sondern R².

affairs %>% 
  select(age, yearsmarried, education, religiousness, rating, children, gender, occupation) %>%  
  map(~lm(affairs ~ .x, data = affairs)) %>% 
  map(summary) %>% 
  map_dbl("r.squared") %>% 
  tidy %>% 
  arrange(desc(x)) %>% 
  rename(r.squared = x) -> modell

## Warning: 'tidy.numeric' ist veraltet.
## Siehe help("Deprecated")

kable(modell)

names	r.squared
rating	0.0781272
yearsmarried	0.0349098
religiousness	0.0208806
children	0.0108181
age	0.0090701
occupation	0.0024613
gender	0.0001377
education	0.0000059

Der map Befehl sieht hier anders aus, als der beim t-Test verwendete, ist aber nur eine andere Schreibweise. Hier die beiden Varianten gegenüber gesellt:

map(~lm(affairs ~ .x, data = affairs))
map(function(x) lm(affairs$affairs ~ .x))

Zur Überprüfung wird eine Regression manuell durchgeführt.

lm1 <- lm(affairs ~ rating, data = affairs)
summary(lm1)$r.squared

## [1] 0.07812718

Wir sehen das gleiche R² wie bei der Ausgabe kable(modell).

Wie viele Regressionen wurden eigentlich durchgeführt?

ncol(affairs %>% 
       select(age, yearsmarried, education, religiousness, rating, children, gender, occupation))

## [1] 8

Insgesamt 8 Stück. Es hat sich also bereits gelohnt die map Funktion anzuwenden. Die Ergebnisse sollen nun noch schön graphisch dargestellt werden.

ggplot(modell, aes(x = reorder(names, r.squared), y = r.squared)) + 
  geom_point(size = 5, color = "green") +
  ylab(expression(R^{2})) +
  xlab("Prädiktoren") +
  ggtitle("Erklärte Varianz pro Prädiktor")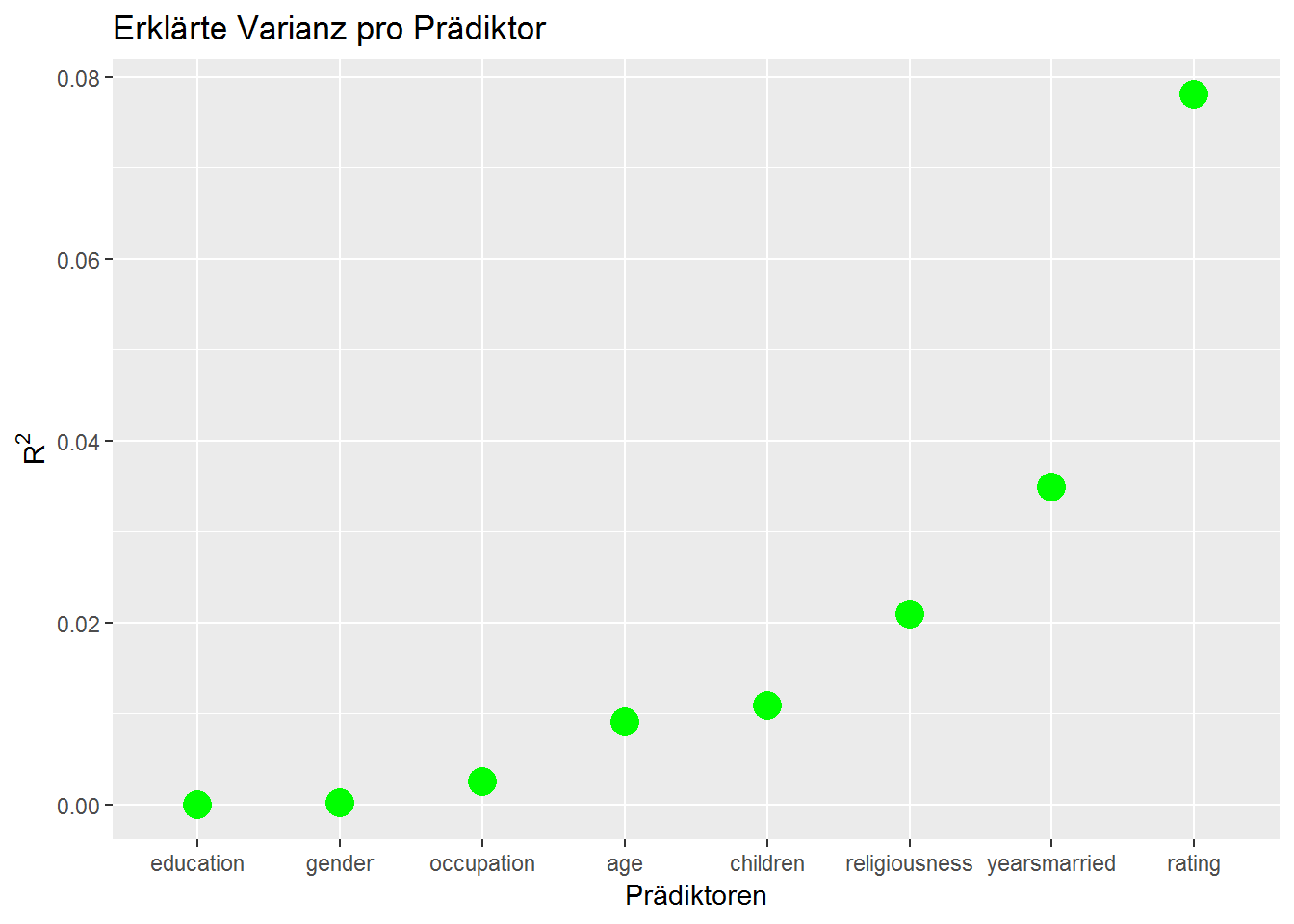

Der Prädiktor rating erklärt also mit knapp 8% am meisten Varianz.

Im zweiten Schritt soll noch überprüft werden, ob die Ergebnisse signifikant sind.

affairs %>% 
  select(age, yearsmarried, education, religiousness, rating, children, gender, occupation) %>%  
  map(~lm(affairs ~ .x, data = affairs)) %>% 
  map(summary) %>%
  map(c("coefficients")) %>% 
  map_dbl(8)  %>%
  tidy %>% 
  arrange(desc(x)) %>% 
  rename(p.value = x) -> modell.pvalue

## Warning: 'tidy.numeric' ist veraltet.
## Siehe help("Deprecated")

kable(modell.pvalue)

names	p.value
education	0.9524501
gender	0.7740138
occupation	0.2245709
age	0.0195320
children	0.0107275
religiousness	0.0003797
yearsmarried	0.0000040
rating	0.0000000

Eine Gegenüberstellung der Ergebnisse kann folgendermaßen aussehen:

cbind(modell, modell.pvalue)

##           names    r.squared         names      p.value
## 1        rating 7.812718e-02     education 9.524501e-01
## 2  yearsmarried 3.490982e-02        gender 7.740138e-01
## 3 religiousness 2.088064e-02    occupation 2.245709e-01
## 4      children 1.081809e-02           age 1.953203e-02
## 5           age 9.070125e-03      children 1.072749e-02
## 6    occupation 2.461327e-03 religiousness 3.797263e-04
## 7        gender 1.377396e-04  yearsmarried 3.995520e-06
## 8     education 5.941117e-06        rating 3.002385e-12

Dies ist allerdings sehr unschön, da die Reihenfolge der beiden Listen mit absteigenden R² bzw p-Wert angefordert wurden und daher unterschiedlich angeordnet sind. Abhilfe leistet hier der left_join Befehl.

Gute_Ansicht <- modell %>% left_join(modell.pvalue, by = "names") %>%
         mutate(P_Wert = round(p.value, digits = 2)) %>%
          select(-p.value)
Gute_Ansicht

## # A tibble: 8 x 3
##   names          r.squared P_Wert
##   <chr>              <dbl>  <dbl>
## 1 rating        0.0781       0   
## 2 yearsmarried  0.0349       0   
## 3 religiousness 0.0209       0   
## 4 children      0.0108       0.01
## 5 age           0.00907      0.02
## 6 occupation    0.00246      0.22
## 7 gender        0.000138     0.77
## 8 education     0.00000594   0.95

6 Conclusion

Die Verwendung der map Funktion ist mit ein wenig Übung leicht anzuwenden und unglaublich effektiv, wenn es um automatisierte Datenanalyse geht.

Automation and Iteration