Table of Content

1 Introduction
2 Preparation
3 Bivariate linear regression
3.1 Unstandardized regression coefficients
3.2 Standardized regression coefficients
3.3 Significance tests
3.4 Confidence interval
3.5 Predicted values
4 Multiple linear regression
4.1 Multiple correlation
4.2 Hierarchical regression
4.3 Gradual regression
5 Model assumption
6 Partial correlation and semi partial correlation
6.1 Partial correlation
6.2 Semi partial correlation
7 Conclusion

1 Introduction

Mit einer Regressionsanalyse wird der Zusammenhang zwischen einer oder mehrerer unabhängigen Variablen und einer abhängigen Variablen ermittelt. In diesem Beitrag wird nachfolgend sowohl die Verwendung der bivariaten linearen Regression als auch die Verwendung der multiplen linearen Regression thematisiert.

Für diesen Post wurde der Datensatz World Happiness Report von der Statistik Plattform “Kaggle” verwendet. Eine Kopie des Datensatzes ist unter https://drive.google.com/open?id=1DLZ_gVFhsT0dBROLE79h2Y5_6NXRF2Br abrufbar.

library(ppcor)
library(tidyverse)
library(psych)
library(car)
library(QuantPsyc)

happiness.report <- read_csv("World_Happiness_Report.csv")

2 Preparation

Für die nachfolgenden Tests sind nicht alle Variablen aus dem Datensatz World Happiness Report relevant. Er wird daher auf folgende 5 reduziert.

Tipp: Mit der select Funktion lassen sich Spalten auch gleichzeitig umbenennen. Dies ist in unserem Fall teilweise auch sinnvoll, da die ursprüngliche Spaltenbezeichnung recht lang ausfällt.

happiness <- happiness.report %>% select(Score = Happiness.Score, Life.exp = Health..Life.Expectancy., Freedom, Generosity, Trust = Trust..Government.Corruption.)
happiness

## # A tibble: 155 x 5
##    Score Life.exp Freedom Generosity Trust
##    <dbl>    <dbl>   <dbl>      <dbl> <dbl>
##  1  7.54    0.797   0.635      0.362 0.316
##  2  7.52    0.793   0.626      0.355 0.401
##  3  7.50    0.834   0.627      0.476 0.154
##  4  7.49    0.858   0.620      0.291 0.367
##  5  7.47    0.809   0.618      0.245 0.383
##  6  7.38    0.811   0.585      0.470 0.283
##  7  7.32    0.835   0.611      0.436 0.287
##  8  7.31    0.817   0.614      0.500 0.383
##  9  7.28    0.831   0.613      0.385 0.384
## 10  7.28    0.844   0.602      0.478 0.301
## # ... with 145 more rows

Score bezeichnet den allgemeinen Glücklichkeitsgrad des jeweiligen Landes.

Life.exp beschreibt das Ausmaß, in wie weit die Lebenserwartung zur Berechnung des Zufriedenheitsgrades beigetragen hat.

Freedom beschreibt das Ausmaß, in wie weit Freiheit zur Berechnung des Zufriedenheitsgrades beigetragen hat.

Generosity beschreibt das Ausmaß, in wie weit Großzügigkeit zur Berechnung des Zufriedenheitsgrades beigetragen hat.

Trust beschreibt das Ausmaß, in wie weit Vertrauen zur Berechnung des Zufriedenheitsgrades beigetragen hat.

Es wird noch überprüft, ob fehlende Werte in der neuen Auswahl existieren.

any(is.na(happiness))

## [1] FALSE

sum(any(is.na(happiness)))

## [1] 0

Das Objekt “happiness” enthält somit keine fehlenden Werte.

3 Bivariate linear regression

Bei der bivariaten linearen Regression wird der lineare Zusammenhang zwischen einer unabhängigen Variablen und einer abhängigen Variablen modelliert. Beide Variablen müssen dafür metrisch skaliert sein.

Die Formel für die bivariate lineare Regression lautet: \[ Y = b_0 + b_1 \cdot X + E \]

Das Regressionsgewicht b₁ sagt aus, welche Veränderung man in Y erwartet, wenn X um eine Einheit erhöht wird. Es ist daher ein Zusammenhangsmaß zwischen X und Y. Der Achsenabschnitt b₀ ist der vorhergesagte Wert für Y, wenn X den Wert Null annimmt.

Zusammenhänge lassen sich auch prima mit Streudiagrammen graphisch darstellen.

plot(happiness$Life.exp, happiness$Score)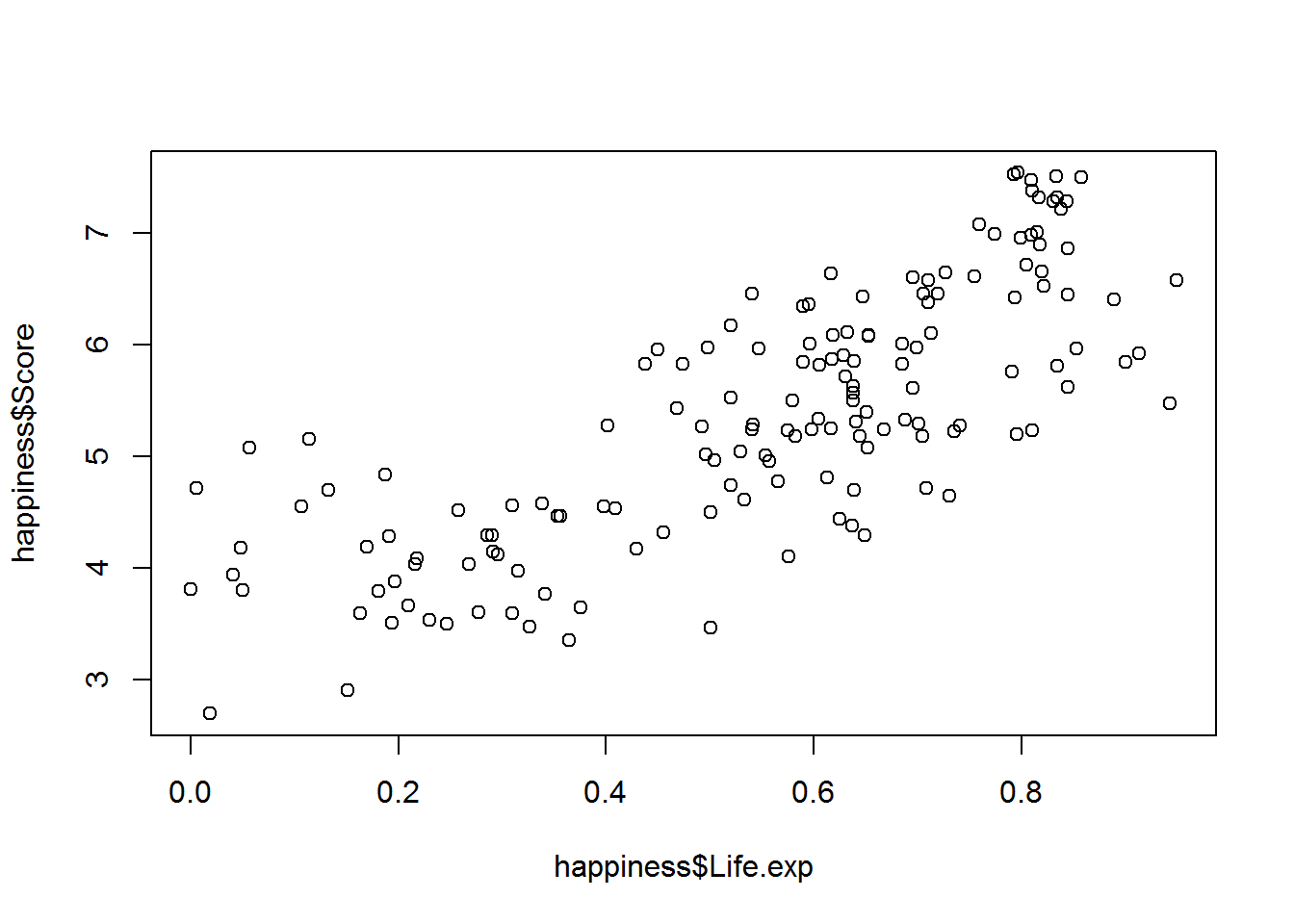

In die plot Funktion kann auch direkt ein statistisches Modell eingeben werden. Allerdings ändert sich hierbei die Reihenfolge des Befehls.

plot(happiness$Score ~ happiness$Life.exp)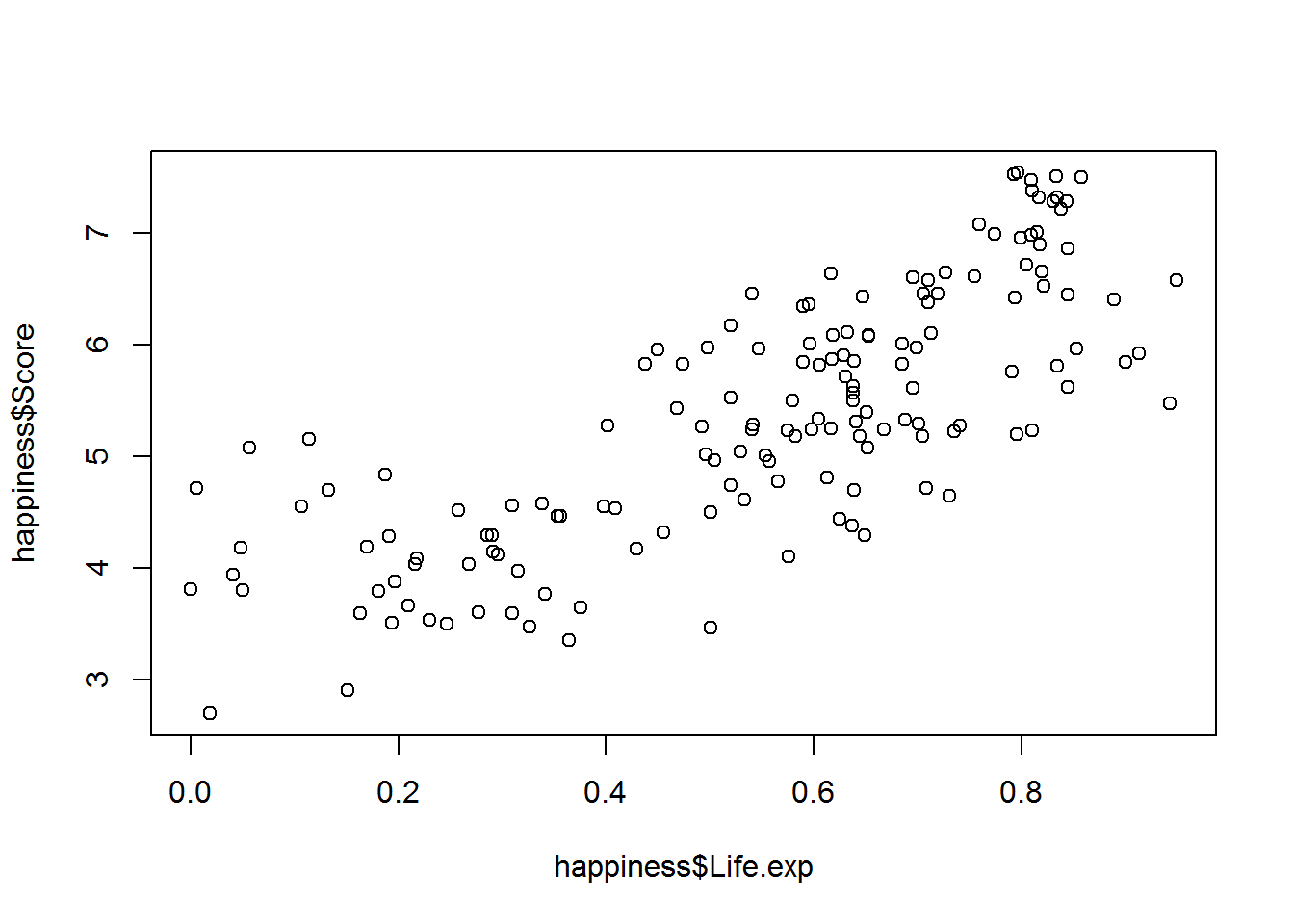

Des Weiteren hat man die Möglichkeit, eine Lowess-Kurve sowie eine Regressionsgerade in der Grafik zu ergänzen.

plot(happiness$Score ~ happiness$Life.exp) + 
  lines(lowess(happiness$Score ~ happiness$Life.exp)) +
  abline(lm(happiness$Score ~ happiness$Life.exp))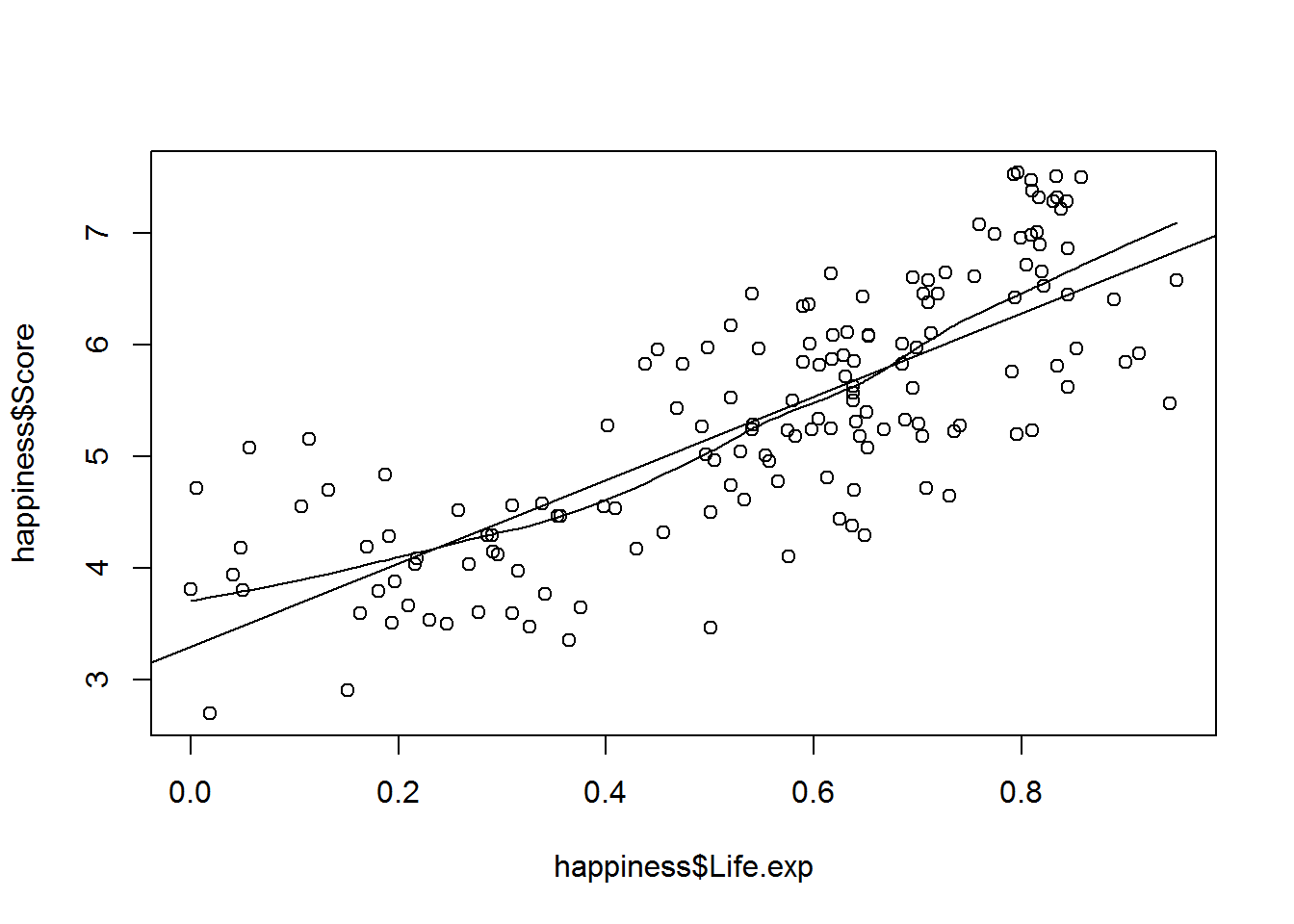

## integer(0)

3.1 Unstandardized regression coefficients

Im Folgenden soll der Zusammenhang zwischen dem Glücklichkeitsgrad (abhängige Variable) und der Lebenserwartung (unabhängige Variable) untersucht werden.

lm(happiness$Score ~ happiness$Life.exp)

## 
## Call:
## lm(formula = happiness$Score ~ happiness$Life.exp)
## 
## Coefficients:
##        (Intercept)  happiness$Life.exp  
##              3.297               3.731

Intercept bedeutet Achsenabschnitt, d.h. b₀ beträgt hier 3,297. Der Wert unter happiness$Life.exp ist das Regressionsgewicht für diese Variable, d.h. b₁ beträgt hier 3,731.

3.2 Standardized regression coefficients

Manchmal ist es sinnvoll, die standardisierten Regressionskoeffizienten anzufordern und zu interpretieren. Dazu werden die verwendeten Variablen z-standardisiert (siehe hierzu Post “z-Transformation / Standardization”). Das Regressionsgewicht b₀ ist dann die Anzahl der Standardabweichungen, um die sich Y verändert, wenn man X um eine Standardabweichung erhöht. Die Standardisierung kann mit der scale Funktion durchgeführt werden.

lm(scale(happiness$Score) ~ scale(happiness$Life.exp))

## 
## Call:
## lm(formula = scale(happiness$Score) ~ scale(happiness$Life.exp))
## 
## Coefficients:
##               (Intercept)  scale(happiness$Life.exp)  
##                -5.574e-16                  7.820e-01

Intercept zeigt einen Wert nahe Null. Dies ist immer so, da die standardisierte Regressionsanalyse durch den Ursprung geht. Das standardisierte Regressionsgewicht beträgt 7.820e-01. Dies ist in R eine andere Schreibweise für 0,782 (Rechenweg s.u.).

\[ 7.820e-01 = 7.820 \cdot 10^{-1} = 7.820 \cdot 0,1 = 0.782 \]

Bei der bivariaten linearen Regressionsanalyse entspricht das standardisierte Regressionsgewicht genau der Korrelation zwischen den beiden Variablen.

cor(happiness$Life.exp, happiness$Score)

## [1] 0.7819506

3.3 Significance tests

Beim Signifikanztest für die Regressionskoeffizienten wird die Nullhypothese (der Regressionskoeffizient ist Null) mit einem t-Test überprüft. Ein signifikantes Ergebnis würde bedeuten, dass sich der Regressionskoeffizient signifikant von Null unterscheidet und somit einen Einfluss auf die abhängige Variable hat.

Wir weisen der zuvor durchgeführten Regression einem Objekt zu und fordern das Ergebnis des Signifikanztests mit der summary Funktion an.

simple.reg <- lm(happiness$Score ~ happiness$Life.exp)
summary(simple.reg)

## 
## Call:
## lm(formula = happiness$Score ~ happiness$Life.exp)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.70245 -0.52220 -0.03812  0.51574  1.56478 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          3.2969     0.1442   22.86   <2e-16 ***
## happiness$Life.exp   3.7312     0.2405   15.52   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7074 on 153 degrees of freedom
## Multiple R-squared:  0.6114, Adjusted R-squared:  0.6089 
## F-statistic: 240.8 on 1 and 153 DF,  p-value: < 2.2e-16

Call zeigt nochmal die Modellgleichung auf.

Residuals beinhaltet 5 statistische Kennwerte für die Residuen.

Coefficients. In diesem Abschnitt wird für jeden Regressionskoeffizienten b (Estimate) der Standardfehler (Std. Error), die empirische Prüfgröße (t value) und der p-Wert (Pr(>|t|)) angegeben.

Residual standard error ist der Standardschätzfehler. Dieser sagt uns, um wie viele Einheiten der abhängigen Variablen wir uns mit der Regression im Durchschnitt verschätzen.

Degrees of freedom sind die Freiheitsgrade. Sie sind definiert mit df=N-k-1, wobei N die Stichprobengröße und k die Anzahl der Prädiktoren ist.

Multiple R-squared. Der Determinationskoeffizient R² mit dem adjustierten R² sowie dem dazugehörigen F-Test.

Wir erhalten ein höchst signifikantes Ergebnis von p < .001 was bedeutet, dass die Lebenserwartung einen Einfluss auf den Glücklichkeitsgrad hat.

Der standardisierte Regressionskoeffizient Beta kann mit der lm.beta Funktion berechnet werden.

lm.beta(simple.reg)

## happiness$Life.exp 
##          0.7819506

3.4 Confidence interval

Konfidenzintervalle für die Regressionsanalyse müssen mit der confint Funktion expliziet angefordert werden.

confint(simple.reg)

##                       2.5 %   97.5 %
## (Intercept)        3.011894 3.581818
## happiness$Life.exp 3.256145 4.206259

Standardgemäße wird ein Konfidenzintervall von 95% ausgegeben. Dies kann mit dem Zusatzargument levels= verändert werden.

confint(simple.reg, level = 0.99)

##                       0.5 %   99.5 %
## (Intercept)        2.920624 3.673087
## happiness$Life.exp 3.103990 4.358413

3.5 Predicted values

Die durch die Regression vorhergesagten Werte können via der fitted Funktion angefordert werden. Die Residuen fordert man über den resid Befehl an. Die Ausführung der beiden Funktionen würde eine vollständige Liste aller vorhergesagten Werte bzw. Residuen ausgeben. Aus diesem Grund werden die Befehle hier nur in Kombination mit der head Funktion angefordert.

head(fitted(simple.reg))

##        1        2        3        4        5        6 
## 6.269379 6.254078 6.407007 6.498717 6.315986 6.321726

head(resid(simple.reg))

##         1         2         3         4         5         6 
## 1.2676211 1.2679223 1.0969934 0.9952833 1.1530137 1.0552734

Man hat hier die Möglichkeit, sich den vorhergesagten Wert für einen bestimmten Wert auf der Prädiktorvariablen ausgeben zu lassen. Im Nachfolgenden soll der vorhergesagte Wert für einen Lebenserwartungswert von 0,8 angefordert werden.

Tipp: Für eine einfache Handhabung sollten die verwendeten Variablen immer Objekten zugeordnet werden. Die Ausführung der predict Funktion funktioniert hierbei zuverlässiger.

Score<-happiness$Score
Life.exp<-happiness$Life.exp

simple.reg2 <- lm(Score ~ Life.exp)

predict(simple.reg2,data.frame(Life.exp=0.8))

##        1 
## 6.281817

Einen Lebenserwartungswert von 0,8 führt zu einem vorhergesagten Glücklichkeitsgrad von 6,28. Nun interessiert uns noch, wie hoch der vorhergesagte Wert für den Mittelwert der Variablen Life.exp ausfällt.

predict(simple.reg2,data.frame(Life.exp=mean(Life.exp)), interval="confidence")

##        fit     lwr      upr
## 1 5.354019 5.24176 5.466279

Der durchschnittliche Lebenserwartungswert in unserem Datensatz führt zu einem Glücklichkeitsgrad von 5,35.

4 Multiple linear regression

Bei der multiplen linearen Regression wird der lineare Zusammenhang zwischen mehreren unabhängigen Variablen und einer abhängigen Variablen modelliert.

Die Formel für die multiple lineare Regression lautet:

\[ Y = b_0 + b_1 \cdot X_1 + b_2 \cdot X_2 + E \]

Der Achsenabschnitt b₀ ist der vorhergesagte Wert für Y, wenn sowohl X₁ als auch X₂ den Wert Null annehmen. Das Regressionsgewicht b₁ ist der Wert, um den sich Y erhöht, wenn man X₁ um eine Einheit erhöht und gleichzeitig X₂ konstant hält. Gleichermaßen dazu ist b₂ der Wert, um den sich Y erhöht, wenn man X₂ um eine Einheit erhöht und gleichzeitig X₁ konstant hält. Die unabhängigen Variablen in dem Modell kontrollieren sich also gegenseitig.

Die multiple lineare Regression wird in R ebenfalls mit der lm Funktion durchgeführt. Im Nachfolgenden soll der Glücklichkeitsgrad durch die Variable ´Life.exp´ und ´Trust´ vorhergesagt werden.

mult.reg <- lm(Score ~ Life.exp + Trust, data = happiness)
summary(mult.reg)

## 
## Call:
## lm(formula = Score ~ Life.exp + Trust, data = happiness)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.95557 -0.43634  0.00548  0.47240  1.66047 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   3.1522     0.1390  22.671  < 2e-16 ***
## Life.exp      3.4266     0.2353  14.565  < 2e-16 ***
## Trust         2.5391     0.5486   4.628 7.85e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6645 on 152 degrees of freedom
## Multiple R-squared:  0.6594, Adjusted R-squared:  0.655 
## F-statistic: 147.2 on 2 and 152 DF,  p-value: < 2.2e-16

Da diese Ausgabe bereits unter Punkt 3.3 ausführlich besprochen wurde, wird nun nur auf zwei Punkte eingegangen:

Multiple R-squared. Dies ist der Determinationskoeffizient R². Er ist ein Maß für die Modellgüte. In dem vorliegenden Beispiel ist R²=.659, was bedeutet, dass die beiden Prädiktoren zusammen 65,9% der beobachteten Varianz in dem Glücklichkeitsgrad erklären.

F-statistic. Der Determinationskoeffizient R² kann inferenzstatistisch geprüft werden. Dies geschieht über den F-Test. In unserem Beispiel zeigt der F-Test ein höchst signifikantes Ergebnis von p<.001, d.h. der Determinationskoeffizient unterscheidet sich signifikant von Null.

4.1 Multiple correlation

Im Post “Bivariate descriptive statistics” (Punkt 3) wurde die Berechnung des Zusammenhangs r zwischen zwei metrischen Variablen gezeigt. Die Höhe des Zusammenhangs r zwischen einer abhängigen Variablen und mehreren unabhängigen Variablen wurde bis jetzt noch nicht thematisiert. Die Berechnung ist allerdings mit der Multiple R-squared Angabe aus dem Ergebnis der Regressionsanalyse möglich. Dazu wird der R² Wert aus der summary-Ausgabe entnommen und anschließend in den sqrt-Befehl eingesetzt.

summary(mult.reg)$r.squared

## [1] 0.6594405

sqrt(summary(mult.reg)$r.squared)

## [1] 0.8120594

Wir können folgende zwei Werte für die Effektgröße der durchgeführten multiplen Regressionsanalyse festhalten:

R² = .659
r = .81

4.2 Hierarchical regression

Anstatt alle Prädiktoren (unabhängige Variablen) auf einmal in das Regressionsmodell aufzunehmen, kann man auch schrittweise vorgehen. Bei der hierarchischen Regression werden die Prädiktoren in zwei oder mehrere Blöcke aufgeteilt und nacheinander in das Modell mit aufgenommen.

Das zentrale statistische Maß bei der hierarchischen Regression ist der Determinationskoeffizient R². Vergleicht man den Determinationskoeffizienten aus dem ersten Modell mit dem Determinationskoeffizienten aus dem zweiten Modell, so kann bestimmt werden, wie viel Varianz die im zweiten Modell hinzugekommenen Prädiktoren über die im ersten Modell aufgenommenen Prädiktoren hinaus erklären. Dieser Zuwachs des Determinationskoeffizienten kann über einen F-Test statistisch überprüft werden. Ein signifikantes Ergebnis würde bedeuten, dass das zweite Modell signifikant mehr Varianz aufklärt als das erste Modell. Ein nicht signifikantes Ergebnis würde demnach bedeuten, dass das zweite Modell nicht signifikant mehr Varianz aufklärt als das erste Modell, obwohl es mehr Prädiktoren enthält. In diesem Fall sollte man das erste Modell bevorzugen.

Für das nachfolgende Beispiel werden zwei Regressionsanalysen erstellt. Das erste Modell enthält zwei Prädiktoren, das zweite enthält drei Prädiktoren.

kleines.modell <- lm(Score ~ Generosity + Freedom, data = happiness)
volles.modell <- lm(Score ~ Generosity + Freedom + Life.exp, data = happiness)

Anschließend werden die jeweiligen Determinationskoeffizienten angefordert.

summary(kleines.modell)$r.squared

## [1] 0.3257483

summary(volles.modell)$r.squared

## [1] 0.7117256

Wir sehen, dass das erste Modell 32,6% der Varianz erklärt und das zweite 71,2%. Es kann nun ausgerechnet werden, dass der Zuwachs in R² gegenüber dem ersten Modell ca. 38,6% beträgt.

klein<-summary(kleines.modell)$r.squared
voll<-summary(volles.modell)$r.squared
voll-klein

## [1] 0.3859773

Nun wird noch überprüft, ob dieser Zuwachs statistisch bedeutsam ist. Der Zuwachs in R² wird mit dem F-Test (anova-Funktion) auf Signifikanz geprüft.

anova(kleines.modell, volles.modell)

## Analysis of Variance Table
## 
## Model 1: Score ~ Generosity + Freedom
## Model 2: Score ~ Generosity + Freedom + Life.exp
##   Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
## 1    152 132.875                                  
## 2    151  56.811  1    76.065 202.18 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Der Zuwachs in R² ist mit p<.001 signifikant. Das bedeutet, dass das zweite Modell mit den drei Prädiktoren signifikant mehr Varianz aufklärt als das erste Modell. Der Prädiktor Lebenserwartung hat einen signifikanten Effekt auf die Kriteriumsvariable.

4.3 Gradual regression

Bei der hierarchischen Regression wurde selber entschieden, welche Prädiktoren in das Modell aufgenommen werden. Bei der schrittweisen Regression wird diese Entscheidung dem Computer überlassen. Es wird hierbei von einer datengeleiteten Auswahl von Prädiktoren gesprochen, bei der in einem schrittweisen Verfahren nach und nach die Prädiktoren in das Modell aufgenommen werden, die das Modell am signifikantesten verbessern. Das daraus resultierende Modell enthält demnach nur Prädiktoren, welche einen signifikanten Effekt auf die Kriteriumsvariable haben.

Es handelt sich hierbei um ein sehr exploratives Vorgehen. Daher sollte stark darauf geachtet werden, welche Prädiktoren bei der schrittweisen Regression zur Auswahl gestellt werden. Würde man alle Variablen der Stichprobe zur Verfügung stellen, so könnten relevante Prädiktoren weggelassen oder irrelevante Prädiktoren aufgenommen werden.

Im ersten Schritt wird das Startmodell definiert. Dieses Modell enthält nur einen Achsenabschnitt.

grad.reg<- lm(Score ~ 1, data = happiness)

Anschließend wird der step-Befehl auf das Startmodell angewendet. Unter dem Argument scope werden alle Prädiktoren aufgelistet, welche berücksichtigt werden sollen.

grad.reg.output <- step(grad.reg, scope = ~ happiness$Life.exp + happiness$Freedom + happiness$Generosity + happiness$Trust)

## Start:  AIC=39.22
## Score ~ 1
## 
##                        Df Sum of Sq     RSS      AIC
## + happiness$Life.exp    1   120.498  76.573 -105.304
## + happiness$Freedom     1    64.059 133.012  -19.713
## + happiness$Trust       1    36.283 160.788    9.683
## + happiness$Generosity  1     4.750 192.321   37.440
## <none>                              197.071   39.222
## 
## Step:  AIC=-105.3
## Score ~ happiness$Life.exp
## 
##                        Df Sum of Sq     RSS      AIC
## + happiness$Freedom     1    19.753  56.820 -149.549
## + happiness$Trust       1     9.458  67.114 -123.739
## + happiness$Generosity  1     2.217  74.356 -107.857
## <none>                               76.573 -105.304
## - happiness$Life.exp    1   120.498 197.071   39.222
## 
## Step:  AIC=-149.55
## Score ~ happiness$Life.exp + happiness$Freedom
## 
##                        Df Sum of Sq     RSS      AIC
## + happiness$Trust       1     1.490  55.330 -151.667
## <none>                               56.820 -149.549
## + happiness$Generosity  1     0.009  56.811 -147.574
## - happiness$Freedom     1    19.753  76.573 -105.304
## - happiness$Life.exp    1    76.192 133.012  -19.713
## 
## Step:  AIC=-151.67
## Score ~ happiness$Life.exp + happiness$Freedom + happiness$Trust
## 
##                        Df Sum of Sq     RSS      AIC
## <none>                               55.330 -151.667
## + happiness$Generosity  1     0.014  55.316 -149.706
## - happiness$Trust       1     1.490  56.820 -149.549
## - happiness$Freedom     1    11.784  67.114 -123.739
## - happiness$Life.exp    1    72.203 127.533  -24.233

Das Informationskriterium AIC wird von R zum Vergleich der verschiedenen Modelle verwendet. Je kleiner der AIC Wert ist, desto besser ist das Modell. Der Tabelle kann entnommen werden, wie die Variablen sich hinsichtlich ihrer Zähler-Quadratsummen (Sum of Sq), Nenner-Quadratsummen (RSS) sowie ihres AIC-Wertes (AIC) verändern würden, wenn diese Variable in das Modell aufgenommen würde.

Das finale Modell wird mit der summary Funktion angefordert.

summary(grad.reg.output)

## 
## Call:
## lm(formula = Score ~ happiness$Life.exp + happiness$Freedom + 
##     happiness$Trust, data = happiness)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.93833 -0.39221  0.02576  0.45721  1.39692 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          2.6019     0.1596  16.307  < 2e-16 ***
## happiness$Life.exp   3.1092     0.2215  14.037  < 2e-16 ***
## happiness$Freedom    2.1997     0.3879   5.671 7.01e-08 ***
## happiness$Trust      1.1260     0.5585   2.016   0.0455 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6053 on 151 degrees of freedom
## Multiple R-squared:  0.7192, Adjusted R-squared:  0.7137 
## F-statistic: 128.9 on 3 and 151 DF,  p-value: < 2.2e-16

5 Model assumption

Es sollten eine Reihe von Annahmen erfüllt sein, damit die lineare Regressionsanalyse korrekte Ergebnisse liefert. Die wichtigsten sind:

Korrekte Spezifikation des Modells
Normalverteilung der Residuen
Homoskedastizität
Ausreißer und einflussreiche Werte
Multikollinearität
Unabhängigkeit der Residuen

Die ersten vier Annahmen können in R mit verschiedenen Diagrammen graphisch geprüft werden. Dies soll exemplarisch mit der multiplen Regression (Punkt 4) durchgeführt werden.

par(mfrow= c(2,2))
plot(mult.reg)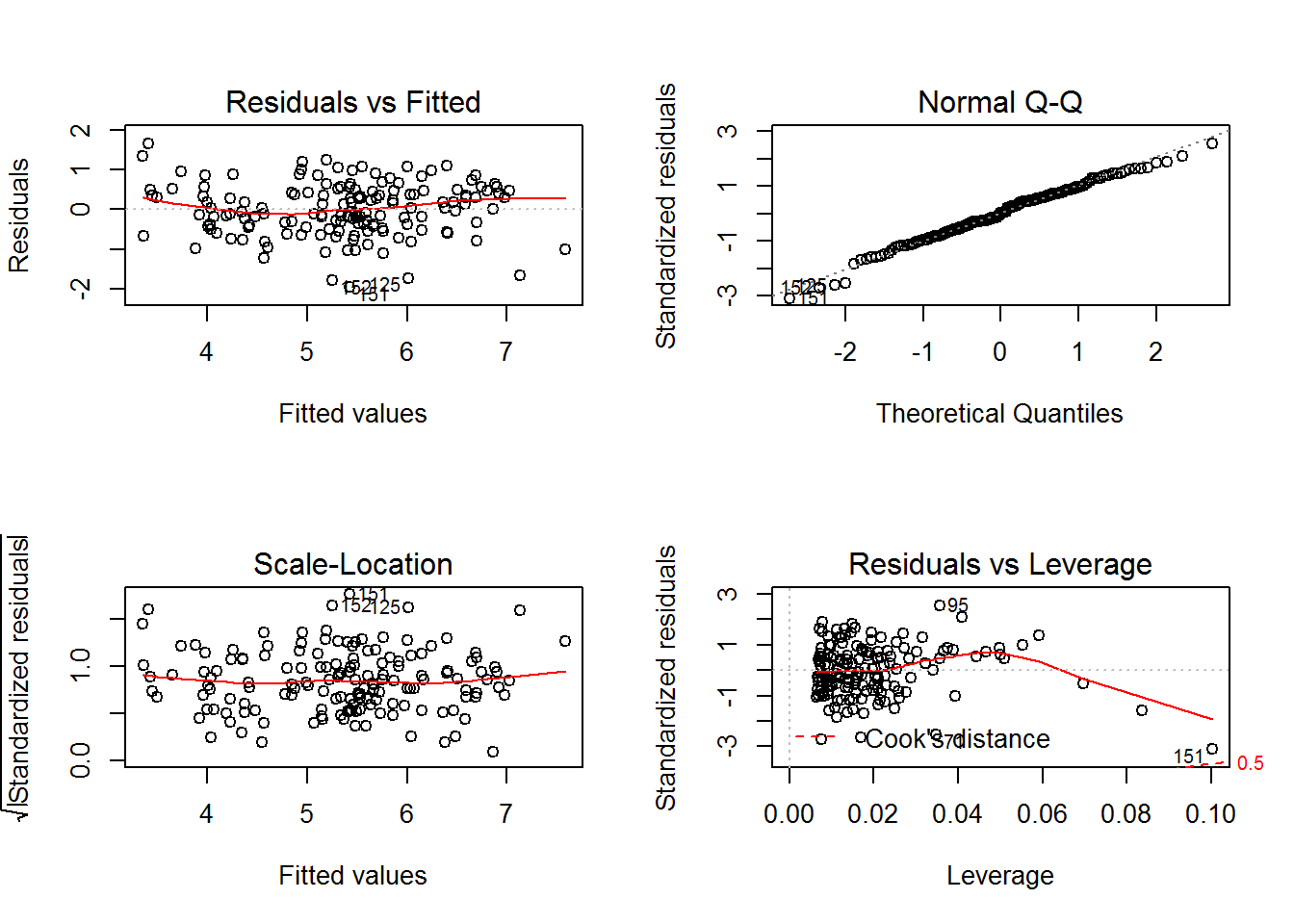

Korrekte Spezifikation des Modells

Hier wird der Frage nachgegangen, ob das Modell alle relevanten und keine überflüssigen Prädiktoren enthält. Das Diagramm “Residuals vs Fitted” (links oben) zeigt die vorhergesagten Werte (fitted values) auf der x-Achse und die unstandardisierten Residuen (residuals) auf der y-Achse. Die rote Linie ist die Lowess-Linie. Dieser Grafik kann entnommen werden, ob das Modell korrekt spezifiziert wurde. Dies ist der Fall, wenn die Werte möglichst unsystematisch verteilt sind und die rote Lowess-Linie möglichst parallel zur x-Achse verläuft. Das Diagramm gibt allerdings keine Aussage darüber, ob wichtige Kontrollvariablen im Modell fehlen.

Normalverteilung der Residuen

Hier wird der Frage nachgegangen, ob die Residuen normalverteilt sind. Dies kann im “Normal Q-Q” Plot (rechts oben) überprüft werden. Auf der x-Achse sind die Quantile abgetragen, die man erwarten würde, wenn Normalverteilung gegeben ist. Auf der y-Achse werden die tatsächlich beobachteten Quantile aufgeführt. Wenn die Residuen normalverteilt sind, liegen sie genau auf der Diagonalen.

Homoskedastizität

Die Homoskedastizität beschreibt, ob die Varianz der Residuen über alle Ausprägungen der Prädiktoren hinweg gleich ist. Die “Scale-Location” Grafik (links unten) dient zur Überprüfung der Homoskedastizität. In diesem Diagramm werden die vorhergesagten Werte (fitted values) auf der x-Achse und die standardisierten Residuen (standardized residuals) auf der y-Achse abgetragen. Homoskedastizität ist dann gegeben, wenn die Residuen weitestgehend unsystematisch im Diagramm verteilt sind.

Ausreißer und einflussreiche Werte

Hier wird überprüft, ob es Ausreißer oder andere Datenpunkte gibt, die einen starken Einfluss auf die Schätzung haben und diese daher verzerren können. Besonders geeignet zur Identifikation von Ausreißern und einflussreichen Werten ist das “Residuals vs Leverage” Diagramm (rechts unten). Auf der x-Achse dieser Grafik werden die Hebelwerte (Leverage) abgetragen. Hebelwerte sind ein Maß für die Abweichungen einzelner Werte auf den unabhängigen Variablen. An großen Hebelwerten kann man somit Ausreißer erkennen. Ausreißer oder einflussreiche Werte sind aber an sich noch nicht schlimm, solange sie sich einigermaßen konform verhalten. Das heißt, solange sie sich nicht zu sehr von den durch die Regression vorhergesagten Werten abweichen. Die Abweichung ist auf der y-Achse in Form der standardisierten Residuen (standardized residuals) abgetragen. In dem “Residuals vs Leverage” Diagramm kann man also ebenfalls erkennen, ob die Ausreißer auffällige Residuen haben. Die rot gestrichelten Linien im Diagramm markieren bestimmte Werte für Cook’s Distance. Liegen einzelne Werte jenseits dieser gestrichelten Linien, so handelt es sich dabei um Werte, die die Regressionsanalyse in einem hohen Maß beeinflussen.

Multikollinearität

Unter Multikollinearität versteht man die multiple Korrelation eines Prädiktors mit allen anderen Prädiktoren im Modell. Dies geschieht unabhängig davon, wie stark die Prädiktoren jeweils mit der Kriteriumsvariable korrelieren. Das Ausmaß der Multikollinearität wird über die Toleranz und den VIF (Variance Inflation Factor) bestimmt. Die Toleranz besitzt einen Wertebereich von 0 bis 1 und sollte möglichst nahe 1 liegen und nicht kleiner als 0,10 werden. Der Variance Inflation Factor ist der Kehrwert der Toleranz. Auch dieser sollte nahe 1 liegen und nicht größer als 10 werden.

Der VIF wird mit der vif Funktion berechnet.

vif(mult.reg)

## Life.exp    Trust 
## 1.084906 1.084906

Die Berechnung der Toleranz basiert auf dem VIF und erfolgt mit folgendem modifiziertem Befehl.

1/vif(mult.reg)

##  Life.exp     Trust 
## 0.9217388 0.9217388

Multikollinearität ist also nicht gegeben.

Unabhängigkeit der Residuen

Man sollte darauf achten, dass die Unabhängigkeit der Residuen in folgenden beiden Fällen häufig verletzt ist:

wenn die Stichprobe aus mehreren Gruppen bestehen
bei Längsschnittdaten/-studien

Besteht die Gesamtstichprobe aus mehreren Gruppen z.B. bei Schulklassen, ist die Unabhängigkeit der Residuen meist verletzt, da es sich um ein geschachteltes Design handelt. Einzelne Personen lassen sich hierbei eindeutig bestimmten Gruppen zuordnen. Die einzelnen Personen sind ihren Gruppenmitgliedern meist ähnlicher als Personen aus anderen Gruppen. Statistisch erfasst wird diese Ähnlichkeit mit einer Intraklassenkorrelation. Ist diese größer Null , muss man die Gruppenzugehörigkeit in dem Regressionsmodell berücksichtigen. Dies geschieht, wenn man beispielsweise ein Mehrebenenanalyse durchführt.

Bei Längsschnittstudien kann es vorkommen, dass die Ausprägung eines Residuums zu einem bestimmten Messzeitpunkt von den zeitlich früheren Residuen beeinflusst wird. Dies wird auch Autokorrelation der Residuen genannt. Wenn eine solche seriale Abhängigkeit vorliegt, sollten geeignete längsschnittliche Verfahren eingesetzt werden.

6 Partial correlation and semi partial correlation

Die Partialkorrelation und die Semipartialkorrelation sind Koeffizienten zur Beschreibung des Zusammenhangs zwischen zwei Variablen unter Kontrolle einer oder mehrerer Drittvariablen.

6.1 Partial correlation

Die Partialkorrelation quantifiziert den Zusammenhang zwischen zwei Variablen X und Y, wenn der Einfluss einer Drittvariablen Z kontrolliert wird. Die Korrelation wird also um den Effekt einer anderen Variablen bereinigt. Dies hat den Zweck, dass wir Kausalvermutungen überprüfen können.

In R wird die Partialkorrelation über die partial.r Funktion angefordert. Im folgenden Beispiel soll der Zusammenhang zwischen dem Lebenserwartungsgrad (Life.exp) und dem Vertrauensgrad (Trust) berechnet werden, wenn der Glücklichkeitsgrad (Score) auspartialisiert ist. Dazu werden im ersten Schritt die drei Variablen dem Objekt “auswahl” zugeordnet.

auswahl <- data.frame(happiness$Score, happiness$Life.exp, happiness$Trust)

Im zweiten Schritt werden die gerundeten bivariaten Korrelationen nullter Ordnung mit der cor Funktion angefordert.

round(cor(auswahl), 2)

##                    happiness.Score happiness.Life.exp happiness.Trust
## happiness.Score               1.00               0.78            0.43
## happiness.Life.exp            0.78               1.00            0.28
## happiness.Trust               0.43               0.28            1.00

Für den Zusammenhang der Variablen Life.exp und Trust erhalten wir einen Wert von r=.28, was einen eher geringeren Zusammenhang darstellt. Nun wird die Partialkorrelation durchgeführt.

partial.r(auswahl, c(2,3), 1)

## partial correlations 
##                    happiness.Life.exp happiness.Trust
## happiness.Life.exp                1.0            -0.1
## happiness.Trust                  -0.1             1.0

Das erste Argument der partial.r Funktion ist der Name des Data Frames, in dem die drei Variablen enthalten sind. Anschließend werden mit c(2, 3) die Spaltennummern der Variablen genannt, deren Korrelation uns interessiert. Die Variablen Life.exp und Trust wurden hier in den Spalten 2 und 3 gespeichert. Das letzte Argument (“1”) ist die Spaltennummer der Variablen, die auspartialisiert werden soll. Würde man an dieser Stelle mehrere Variablen angeben, würden Partialkorrelationen höherer Ordnung berechnet werden.

Die R-Ausgabe enthält eine Korrelationsmatrix mit der Partialkorrelation. Die Partialkorrelation zwischen den beiden Variablen Life.exp und Trust ist also r=-.1. Im Vergleich zur bivariaten Korrelation hat sich der Zusammenhang durch die Auspartialisierung des Glücklichkeitsgrades von einer geringen positiven Korrelation in eine leicht negative Korrelation verändert.

Leider wird mit der partial.r Funktion kein p-Wert mit ausgegeben. Aus diesem Grund wird eine weitere Möglichkeit zur Berechnung der Partialkorrelation mit dem ppcor Package vorgestellt.

pcor.test(auswahl$happiness.Life.exp, auswahl$happiness.Trust, auswahl$happiness.Score, method = c("pearson"))

##      estimate   p.value statistic   n gp  Method
## 1 -0.09904614 0.2216609 -1.227157 155  1 pearson

Nun wird zusätzlich zu dem Zusammenhang (r=-.1) der Variablen Life.exp und Trust noch der p-Wert von .222 berechnet.

6.2 Semi partial correlation

Die Semipartialkorrelation quantifiziert den Zusammenhang zwischen zwei Variablen X und Y, wenn der Einfluss einer Drittvariablen Z aus nur einer der beiden Variablen auspartialisiert wird. Dabei kann überprüft werden, ob ein Prädiktor zusätzliche Informationen bei der Erklärung des Kriteriums besitzt.

Die Partialkorrelation entspricht formal der Korrelation der Regressionsresiduen, die man erhält, wenn man die interessierende Variablen X und Y jeweils aus Z vorhersagt. Bei der Semipartialkorrelation wird die Regressionsanalyse für nur eine der beiden Variablen durchgeführt. Anschließend werden diese Regressionsresiduen mit den beobachteten Werten der anderen Variablen korreliert.

Im folgenden Beispiel soll die Semipartialkorrelation zwischen dem Glücklichkeitsgrad (Score) und dem Lebenserwartungsgrad (Life.exp) berechnet werden, wobei der Vertrauensgrad (Trust) aus dem Lebenserwartungsgrad (Life.exp) auspartialisiert werden soll. Dafür wird eine Regression mit dem Lebenserwartungsgrad als abhängige Variable und dem Vertrauensgrad als unabhängige Variable durchgeführt. Mit der resid Funktion werden die Residuen für dieses Modell angefordert, welche wir unter dem Objekt “auswahl2” abspeichern.

auswahl2<- resid(lm(happiness.Life.exp ~ happiness.Trust, data = auswahl))

Anschließend wird die Korrelation zwischen dem Glücklichkeitsgrad (Score) und der neuen Variablen “auswahl2” berechnet. Dies stellt dann die gewünschte Semipartialkorrelation da.

cor(auswahl$happiness.Score, auswahl2)

## [1] 0.6894426

7 Conclusion

In diesem Post wurde die Anwendung der bivariaten linearen Regression und die Anwendung für die multiple lineare Regression behandelt. Es wurden Effektgrößen für die Regressionsanalyse berechnet und die Prüfung einiger Modellannahmen gezeigt. Abschließend wurde auf die Funktionsweise der Partial- und Semipartialkorrelation eingegangen.

Source

Luhmann, M. (2011). R für Einsteiger.

Regression Analysis