Table of Content

1 Introduction
2 Preparation
3 Essential requirements
3.1 Normal distribution
3.2 Sampling size
3.3 Homogeneity of variance
4 MANOVA
5 Interaction diagram
6 Post-hoc-method
7 Effect size
8 Conclusion

1 Introduction

Aufbauend auf den Post “ANOVA”, in dem es um die Funktionsweise der einfaktoriellen Varianzanalyse ging, soll nachfolgend das Prinzip der mehrfaktoriellen Varianzanalyse ohne Messwiederholung, kurz MANOVA (multivariate analysis of variance), näher erläutert werden. Im Gegensatz zur einfaktoriellen Varianzanalyse werden bei der MANOVA nicht nur eine, sondern mehrere unabhängige Variablen betrachtet.

Für diesen Post wurde der Datensatz World Happiness Report von der Statistik Plattform “Kaggle” verwendet. Eine Kopie des Datensatzes ist unter https://drive.google.com/open?id=1DLZ_gVFhsT0dBROLE79h2Y5_6NXRF2Br abrufbar.

library(tidyverse)
library(psych)
library(sjstats)
library(nortest)
library(car)
library(gplots)
library(MBESS)

Happiness <- read_csv("World_Happiness_Report.csv")

2 Preparation

Anhand des Datensatzes World Happiness Report soll eine zweifaktorielle Varianzanalyse durchgeführt werden. Dafür kreieren wir im ersten Schritt zwei unabhängige kategoriale Variablen (zwei Faktoren).

Happiness$Family.new <- ifelse(Happiness$Family >= 1.254, "viele.Familien", "weniger.Familien")
Happiness$Freedom.new <- ifelse(Happiness$Freedom >= 0.4375, "viel.Freiheit", "weniger.Freiheit")

Für das folgende Beispiel wurden die Faktoren Family.new und Freedom.new erstellt. Die Variable Family.new beschreibt nun die Länder im Datensatz mit den beiden Ausprägungen “viele.Familien” und “weniger.Familien” und die Variable Freedom.new mit den beiden Ausprägungen “viel.Freiheit” und “weniger.Freiheit”. Aufgeteilt wurden die beiden Variablen jeweils nach ihrem Median.

median(Happiness$Family)

## [1] 1.253918

median(Happiness$Freedom)

## [1] 0.4374543

Die abhängige Variable für die MANOVA soll der Happiness.Score sein.

glimpse(Happiness)

## Observations: 155
## Variables: 14
## $ Country                       <chr> "Norway", "Denmark", "Iceland", ...
## $ Happiness.Rank                <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 1...
## $ Happiness.Score               <dbl> 7.537, 7.522, 7.504, 7.494, 7.46...
## $ Whisker.high                  <dbl> 7.594445, 7.581728, 7.622030, 7....
## $ Whisker.low                   <dbl> 7.479556, 7.462272, 7.385970, 7....
## $ Economy..GDP.per.Capita.      <dbl> 1.616463, 1.482383, 1.480633, 1....
## $ Family                        <dbl> 1.533524, 1.551122, 1.610574, 1....
## $ Health..Life.Expectancy.      <dbl> 0.7966665, 0.7925655, 0.8335521,...
## $ Freedom                       <dbl> 0.6354226, 0.6260067, 0.6271626,...
## $ Generosity                    <dbl> 0.36201224, 0.35528049, 0.475540...
## $ Trust..Government.Corruption. <dbl> 0.31596383, 0.40077007, 0.153526...
## $ Dystopia.Residual             <dbl> 2.277027, 2.313707, 2.322715, 2....
## $ Family.new                    <chr> "viele.Familien", "viele.Familie...
## $ Freedom.new                   <chr> "viel.Freiheit", "viel.Freiheit"...

table(Happiness$Family.new)

## 
##   viele.Familien weniger.Familien 
##               77               78

table(Happiness$Freedom.new)

## 
##    viel.Freiheit weniger.Freiheit 
##               77               78

3 Essential requirements

Die Voraussetzungen für die MANOVA sind die gleichen wie bei der einfaktoriellen Varianzanalyse. Diese waren:

Unabhängigkeit der Messungen. Kein Teilnehmer aus einer Gruppe darf auch in einer anderen Gruppe vorkommen.
Die abhängige Variable ist metrisch skaliert.
Die unabhängige Variable ist unabhängig und nominalskaliert.
Normalverteilung der abhängigen Variablen in allen Populationen, wenn gilt N < 30 in jeder Population.
Varianzhomogenität der abhängigen Variablen in allen Populationen.

3.1 Normal distribution

Für die Überprüfung der Normalverteilung der abhängigen Variable, wird wie gewohnt der Lilliefors-Test angewendet.

lillie.test(Happiness$Happiness.Score)

## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  Happiness$Happiness.Score
## D = 0.050105, p-value = 0.4458

Mit p > .446 ist die Variable Happiness.Score normalverteilt.

3.2 Sampling size

desc.Hauptfaktor1 <- describeBy(Happiness$Happiness.Score, Happiness$Family.new, mat = TRUE)
desc.Hauptfaktor2 <- describeBy(Happiness$Happiness.Score, Happiness$Freedom.new, mat = TRUE)
desc.Hauptfaktor1

##     item           group1 vars  n     mean        sd median  trimmed
## X11    1   viele.Familien    1 77 6.110429 0.8677820 6.0980 6.139175
## X12    2 weniger.Familien    1 78 4.607308 0.8240891 4.5515 4.602781
##          mad   min   max range        skew   kurtosis         se
## X11 0.896973 4.096 7.537 3.441 -0.26249300 -0.6588109 0.09889293
## X12 1.002238 2.693 6.578 3.885  0.03968612 -0.7186485 0.09330972

desc.Hauptfaktor2

##     item           group1 vars  n     mean        sd median  trimmed
## X11    1    viel.Freiheit    1 77 5.860519 1.0493845  5.956 5.890317
## X12    2 weniger.Freiheit    1 78 4.854013 0.9811528  4.790 4.838563
##          mad   min   max range       skew   kurtosis        se
## X11 1.128258 3.471 7.537 4.066 -0.2165218 -0.9094135 0.1195885
## X12 1.088228 2.693 7.213 4.520  0.0696700 -0.7288668 0.1110937

Da die beiden unabhängigen Variablen Family.new und Freedom.new jeweils nach ihrem Median aufgeteilt wurden, sind die 4 Gruppen fast gleich groß.

3.3 Homogeneity of variance

leveneTest(Happiness$Happiness.Score ~ Happiness$Family.new * Happiness$Freedom.new)

## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value Pr(>F)
## group   3  0.2885 0.8337
##       151

Mit p > .834 ist Varianzhomogenität innerhalb der Gruppen gegeben.

4 MANOVA

Auch die mehrfaktorielle Varianzanalyse wird mit dem aov Befehl angefordert. Für unser Beispiel sieht die Syntax folgendermaßen aus:

MANOVA <- aov(Happiness$Happiness.Score ~ Happiness$Family.new * Happiness$Freedom.new)

Wie auch bei der ANOVA wird als erstes Argument die abhängige Variable genannt. Nach der Tilde kommt/kommen die unabhängige/n Variable/n. Alternativ könnte man auch folgende (etwas längere) Syntax verwenden:

alternative.Syntax <- aov(Happiness$Happiness.Score ~ Happiness$Family.new + Happiness$Freedom.new + Happiness$Family.new:Happiness$Freedom.new)

Beschreibung der unterschiedlichen Mittelwerte

Für die Ausgabe der unterschiedlichen Mittelwerte kann erneut die model.tables Funktion angewendet werden.

model.tables(MANOVA, "means")

## Tables of means
## Grand mean
##          
## 5.354019 
## 
##  Happiness$Family.new 
##     viele.Familien weniger.Familien
##               6.11            4.607
## rep          77.00           78.000
## 
##  Happiness$Freedom.new 
##     viel.Freiheit weniger.Freiheit
##             5.553            5.157
## rep        77.000           78.000
## 
##  Happiness$Family.new:Happiness$Freedom.new 
##                     Happiness$Freedom.new
## Happiness$Family.new viel.Freiheit weniger.Freiheit
##     viele.Familien    6.30          5.66           
##     rep              54.00         23.00           
##     weniger.Familien  4.82          4.52           
##     rep              23.00         55.00

Grand mean beschreibt wieder den Gesamtmittelwert. Die Tabelle Happiness.Family.new zeigt die Mittelwerte (der Variable Happiness.Score) für alle Länder mit vielen und wenigen Familien, umabhängig davon, ob diese einen hohen oder niedrigen “Freedom”-Grad haben. Die Zeile rep nennt uns die Stichprobengröße. In der Tabelle Happiness.Freedom.new erhalten wir die Mittelwerte und Stichprobengrößen für alle Länder (aufgeteilt nach den beiden Kategorien “viel.Freiheit” und “weniger.Freiheit”), unabhängig davon, ob diese einen hohen oder niedrigen “Family”-Grad haben. Schließlich werden in der Tabelle Happiness.Family.new:Happiness.Freedom.new die Stichprobengrößen und Mittelwerte für jede der einzelnen Kombinationen ausgegeben.

Verschiedene Quadratsummentypen

Das Ergebnis der ANOVA wurde mit der summary Funktion angefordert (siehe Post “ANOVA” Punkt 4). Mittels dieser Funktion wird in R automatisch Typ-I-Quadratsummen berechnet. Die Typ-III-Quadratsummen gelten als besser interpretierbar, weshalb sie in diesem Beispiel auch speziell angefordert werden. Dies ist mit der Funktion Anova und dem Zusatzargument typ = 3) möglich. Beim Typ-III-Modell wird der Interaktionseffekt von Anfang an bei der Evaluierung mitberücksichtigt.

Anova(MANOVA, type=3)

## Anova Table (Type III tests)
## 
## Response: Happiness$Happiness.Score
##                                             Sum Sq  Df  F value    Pr(>F)
## (Intercept)                                2145.67   1 3198.336 < 2.2e-16
## Happiness$Family.new                         35.48   1   52.888 1.781e-11
## Happiness$Freedom.new                         6.74   1   10.049  0.001846
## Happiness$Family.new:Happiness$Freedom.new    0.96   1    1.429  0.233806
## Residuals                                   101.30 151                   
##                                               
## (Intercept)                                ***
## Happiness$Family.new                       ***
## Happiness$Freedom.new                      ** 
## Happiness$Family.new:Happiness$Freedom.new    
## Residuals                                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Die Bedeutung der einzelnen Spalten wurde bereits im Post “ANOVA” (unter Punkt 4) genau erklärt. Wir erhalten ein höchst signifikantes Ergebnis für den Haupteffekt des Faktors Family.new (p < .001) und ein hoch signifikantes Ergebnis für den Haupteffekt des Faktors Freedom.new (p = .002). Das Ergebnis für den Interaktionseffekt ist mit p = .23 nicht signifikant.

Die Spalte “Residuals” beinhaltet die Quadratsummen und Freiheitsgrade für den Nenner, beziehungsweise die Unterschiede innerhalb der Gruppen.

5 Interaction diagram

Interaktionseffekte (auch Wechselwirkungseffekte genannt) betrachten die Wirkung eines Faktors (hier Family.new) in Abhängigkeit von einem anderen Faktor (hier Freedom.new). Interaktionseffekte treten dann auf, wenn sich die Wirkung eines Faktors A unterscheidet, je nachdem unter welcher Stufe eines zweiten Faktors B man diesen untersucht. Liegt ein Interaktionseffekt vor bedeutet dies, dass die Wirkung der Faktoren in Kombination über die Summe aus den Einzelwirkungen der Faktoren hinausgeht. Deckt man in einem statistischen Test Wechselwirkungseffekte auf, sollte man diese auch interpretieren. Am einfachsten lassen sich Interaktionen interpretieren, indem man in einem Interaktionsdiagramm die Mittelwerte graphisch darstellt.

Visualisierung der Haupteffekte

Happiness$Family.new.kurz <- ifelse(Happiness$Family.new == "viele.Familien", "viele", "weniger")
Happiness$Freedom.new.kurz <- ifelse(Happiness$Freedom.new == "viel.Freiheit", "viel", "weniger")
par(mfrow=c(1,2))
plotmeans(Happiness$Happiness.Score ~ Happiness$Family.new.kurz, xlab="Familien",
          ylab="Glücklichkeitsgrad", main="Interaktionsplot Faktor Family")
plotmeans(Happiness$Happiness.Score ~ Happiness$Freedom.new.kurz, xlab="Freiheit",
          ylab="Glücklichkeitsgrad", main="Interaktionsplot Faktor Freedom")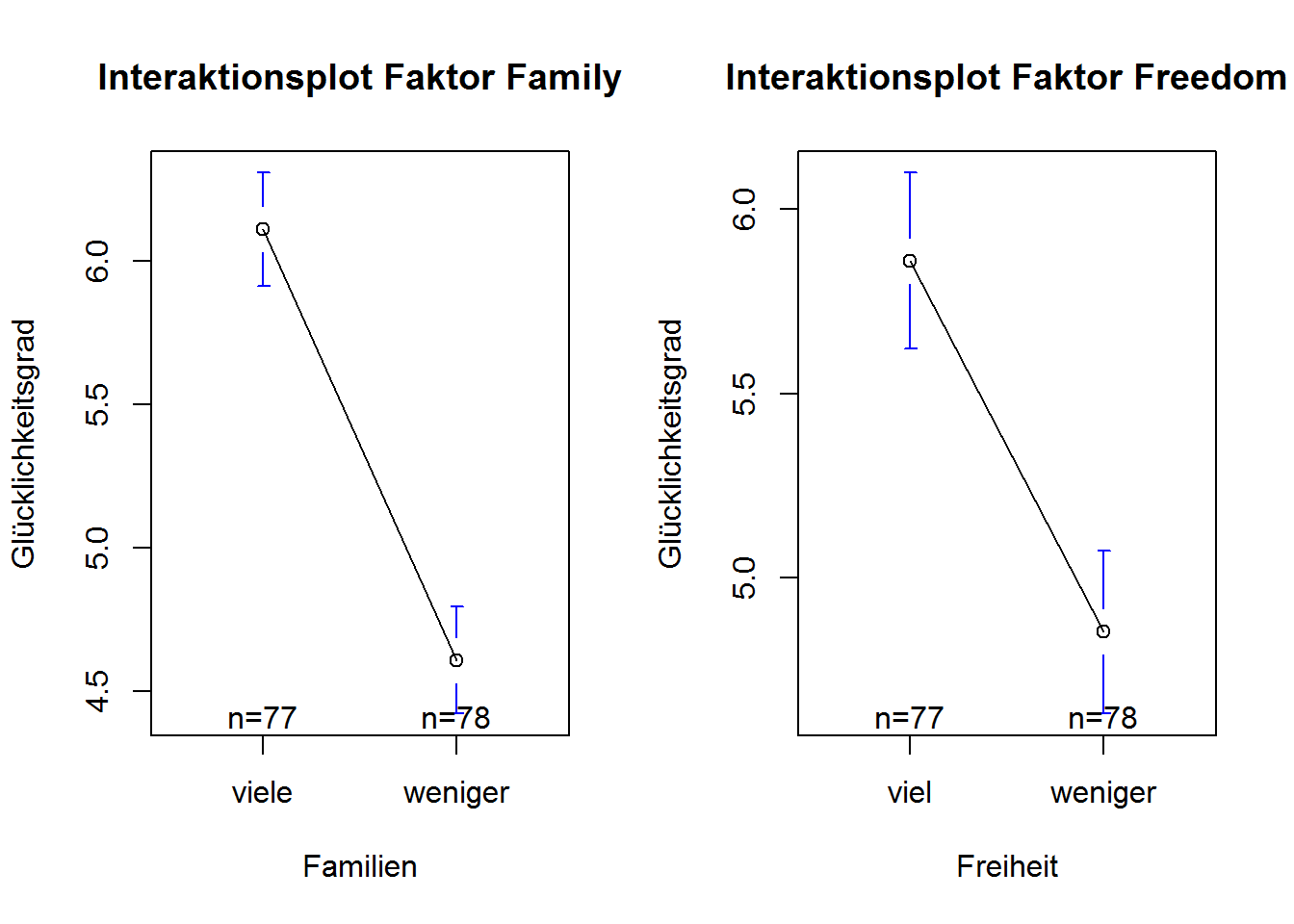

In diesen beiden Diagrammen, werden die Haupteffekte für die Faktoren Family.newund Freedom.new veranschaulicht. Man sieht, dass sich beide Haupteffekte in ihrem mittleren Glücklichkeitsgrad (innerhalb ihrer beiden Ausprägungen viele/weniger Familien und viel/weniger Freiheit) deutlich unterscheiden.

Visualisierung des Interaktionseffekts

Für die graphische Darstellung des Interaktionseffektes wird ein eigener Dataframe, mit den Werten für jede Kombination der Haupteffekte (abzulesen aus der Tabelle Happiness.Family.new:Happiness.Freedom.new), erstellt und in zwei Diagrammen graphisch dargestellt.

model.tables(MANOVA, "means")

## Tables of means
## Grand mean
##          
## 5.354019 
## 
##  Happiness$Family.new 
##     viele.Familien weniger.Familien
##               6.11            4.607
## rep          77.00           78.000
## 
##  Happiness$Freedom.new 
##     viel.Freiheit weniger.Freiheit
##             5.553            5.157
## rep        77.000           78.000
## 
##  Happiness$Family.new:Happiness$Freedom.new 
##                     Happiness$Freedom.new
## Happiness$Family.new viel.Freiheit weniger.Freiheit
##     viele.Familien    6.30          5.66           
##     rep              54.00         23.00           
##     weniger.Familien  4.82          4.52           
##     rep              23.00         55.00

par(mfrow=c(1,1))
Freiheit <- c("viel.Freiheit", "weniger.Freiheit", "viel.Freiheit", "weniger.Freiheit")
Gluecklichkeitsgrad <- c(6.30, 4.52, 4.82, 5.66)
Familien <- c("viele.Familien", "weniger.Familien", "weniger.Familien", "viele.Familien")
Datensatz1 <- data.frame(Freiheit, Gluecklichkeitsgrad, Familien)
colnames(Datensatz1) <- c("Freiheit", "Glücklichkeitsgrad", "Familien")
Datensatz1

##           Freiheit Glücklichkeitsgrad         Familien
## 1    viel.Freiheit               6.30   viele.Familien
## 2 weniger.Freiheit               4.52 weniger.Familien
## 3    viel.Freiheit               4.82 weniger.Familien
## 4 weniger.Freiheit               5.66   viele.Familien

Sicht1 <- ggplot(Datensatz1, aes(x = Freiheit, y = Glücklichkeitsgrad, color = Familien)) + 
  geom_line(aes(group = Familien)) + 
  geom_point() + 
  ggtitle("Interaktionseffekt Sicht 1")


Sicht2 <- ggplot(Datensatz1, aes(x = Familien, y = Glücklichkeitsgrad, color = Freiheit)) + 
  geom_line(aes(group = Freiheit)) + 
  geom_point() + 
  ggtitle("Interaktionseffekt Sicht 2")

Sicht1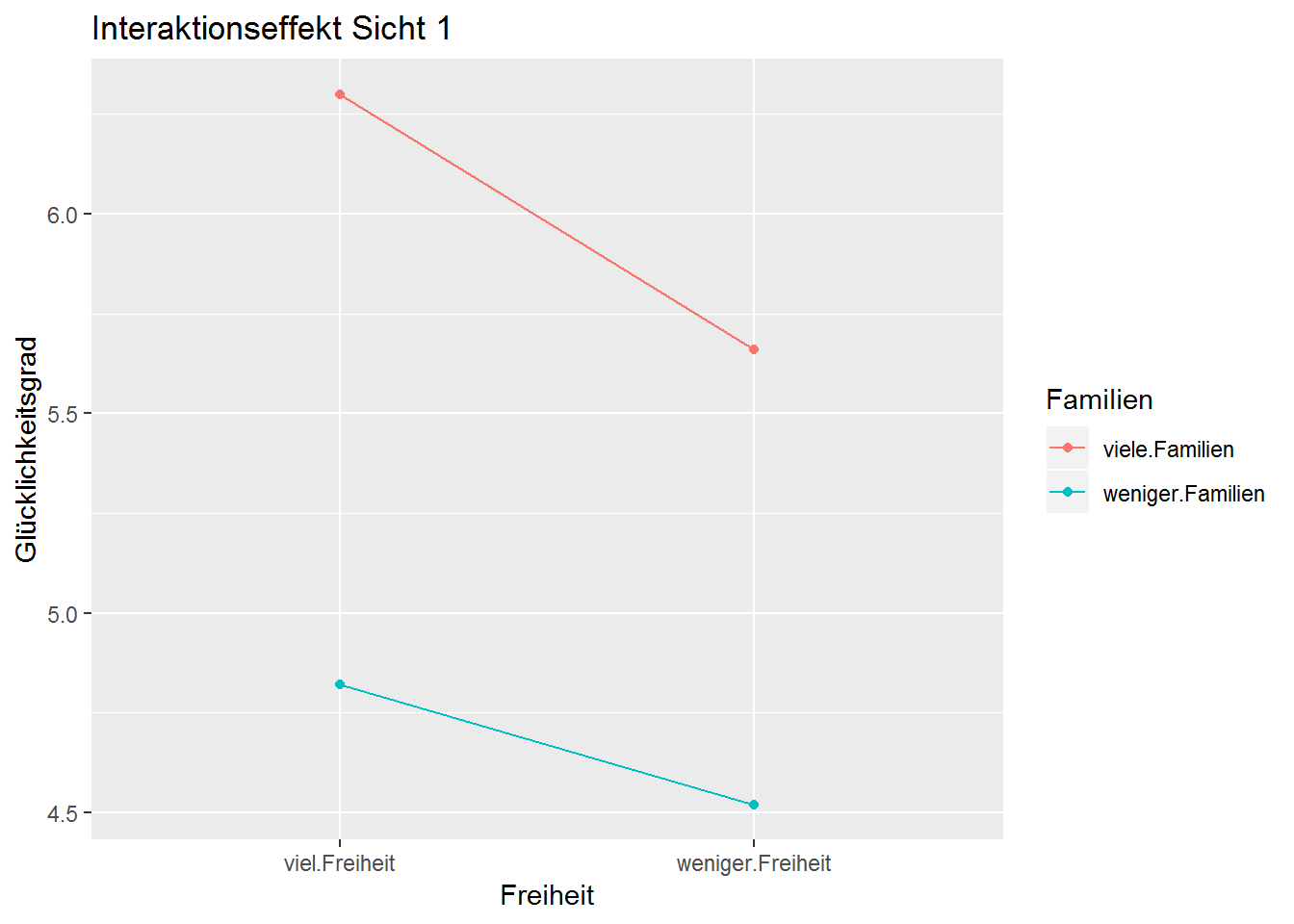

Sicht2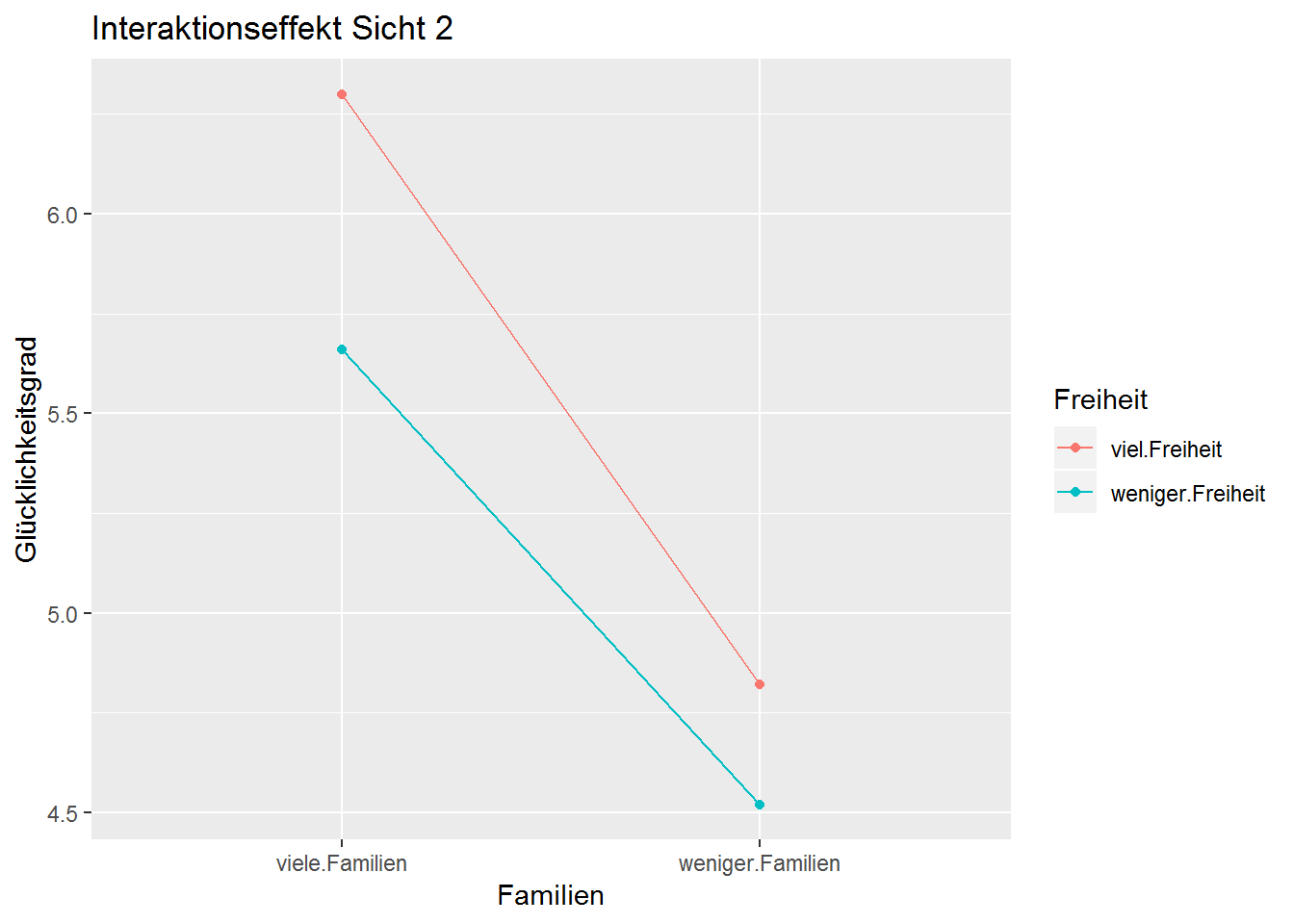

Bei beiden Diagrammen (Sicht1 und Sicht 2) handelt es sich um die selben adjustierten Mittelwerte. Der Unterschied zwischen den Diagrammen ist, dass beim ersten Diagramm (“Interaktionseffekt Sicht 1”) der Faktor “Freiheit” auf der x-Achse abgetragen ist und beim zweiten Diagramm (“Interaktionseffekt Sicht 2”) der Faktor “Familien”.

6 Post-hoc-method

Bei der einfaktoriellen Varianzanalyse ohne Messwiederholung wurde die pairwise.t.test Funktion angewendet, um multiple Paarvergleiche durchzuführen (Post “ANOVA” Punkt 6). Für eine mehrdimensionale Varianzanalyse funktioniert dieser Befehl nicht mehr. Stattdessen, kann die TukeyHSD Funktion verwendet werden.

TukeyHSD(MANOVA)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = Happiness$Happiness.Score ~ Happiness$Family.new * Happiness$Freedom.new)
## 
## $`Happiness$Family.new`
##                                      diff       lwr       upr p adj
## weniger.Familien-viele.Familien -1.503121 -1.763098 -1.243144     0
## 
## $`Happiness$Freedom.new`
##                                      diff       lwr        upr     p adj
## weniger.Freiheit-viel.Freiheit -0.3955979 -0.655575 -0.1356208 0.0030961
## 
## $`Happiness$Family.new:Happiness$Freedom.new`
##                                                                         diff
## weniger.Familien:viel.Freiheit-viele.Familien:viel.Freiheit       -1.4831458
## viele.Familien:weniger.Freiheit-viele.Familien:viel.Freiheit      -0.6464936
## weniger.Familien:weniger.Freiheit-viele.Familien:viel.Freiheit    -1.7853370
## viele.Familien:weniger.Freiheit-weniger.Familien:viel.Freiheit     0.8366522
## weniger.Familien:weniger.Freiheit-weniger.Familien:viel.Freiheit  -0.3021913
## weniger.Familien:weniger.Freiheit-viele.Familien:weniger.Freiheit -1.1388434
##                                                                          lwr
## weniger.Familien:viel.Freiheit-viele.Familien:viel.Freiheit       -2.0129571
## viele.Familien:weniger.Freiheit-viele.Familien:viel.Freiheit      -1.1763049
## weniger.Familien:weniger.Freiheit-viele.Familien:viel.Freiheit    -2.1929722
## viele.Familien:weniger.Freiheit-weniger.Familien:viel.Freiheit     0.2091898
## weniger.Familien:weniger.Freiheit-weniger.Familien:viel.Freiheit  -0.8305619
## weniger.Familien:weniger.Freiheit-viele.Familien:weniger.Freiheit -1.6672141
##                                                                          upr
## weniger.Familien:viel.Freiheit-viele.Familien:viel.Freiheit       -0.9533345
## viele.Familien:weniger.Freiheit-viele.Familien:viel.Freiheit      -0.1166823
## weniger.Familien:weniger.Freiheit-viele.Familien:viel.Freiheit    -1.3777018
## viele.Familien:weniger.Freiheit-weniger.Familien:viel.Freiheit     1.4641146
## weniger.Familien:weniger.Freiheit-weniger.Familien:viel.Freiheit   0.2261794
## weniger.Familien:weniger.Freiheit-viele.Familien:weniger.Freiheit -0.6104728
##                                                                       p adj
## weniger.Familien:viel.Freiheit-viele.Familien:viel.Freiheit       0.0000000
## viele.Familien:weniger.Freiheit-viele.Familien:viel.Freiheit      0.0098774
## weniger.Familien:weniger.Freiheit-viele.Familien:viel.Freiheit    0.0000000
## viele.Familien:weniger.Freiheit-weniger.Familien:viel.Freiheit    0.0038300
## weniger.Familien:weniger.Freiheit-weniger.Familien:viel.Freiheit  0.4485891
## weniger.Familien:weniger.Freiheit-viele.Familien:weniger.Freiheit 0.0000006

Es werden drei Tabellen, mit identischen Spalten ausgegeben.

Die Spalte diff enthält die Mittelwertsdifferenz für den jeweiligen Gruppenvergleich. Die Spalten lwr und upr enthalten die untere bzw. obere Grenze des Konfidenzintervalls für diese Mittelwertsdifferenz. In der Spalte p adj sind die adjustierten p-Werte aufgeführt. Die ersten beiden Tabellen “Happiness.Family.new” und “Happiness.Freedom.new” enthalten die Post-hoc Vergleiche für die beiden Haupteffekte. In der Tabelle “Happiness.Family.new:Happiness.Freedom.new” werden alle vier Einzelgruppen miteinander verglichen (6 paarweise Vergleiche).

7 Effect size

Bei der einfaktoriellen Varianzanalyse wurde die Effektgröße eta² berechnet. Sie drückt den gesamten Anteil der durch alle Effekte erklärten Varianz an der Gesamtvarianz aus. Da wir bei der MANOVA den Beitrag eines bestimmten Effekts zur Gesamtvarianz berechnen wollen, brauchen wir hierfür das partielle eta².

Die Formel für das partielle eta² lautet: \[partielles.eta^2 = \frac{\mathrm{QS}_\mathrm{Effekt}}{\mathrm{QS}_\mathrm{Effekt}+\mathrm{QS}_\mathrm{Fehler}}\]

QS-Effekt steht für die Quadratsummen des Effekts und QS-Fehler für die Quadratsummen des Fehlers. Diese beiden Werte können wieder der Varianzanalysetabelle entnommen werden. Als Beispiel soll nachfolgend das partielle eta² für den Interaktionseffekt berechnet werden.

Anova(MANOVA, type=3)

## Anova Table (Type III tests)
## 
## Response: Happiness$Happiness.Score
##                                             Sum Sq  Df  F value    Pr(>F)
## (Intercept)                                2145.67   1 3198.336 < 2.2e-16
## Happiness$Family.new                         35.48   1   52.888 1.781e-11
## Happiness$Freedom.new                         6.74   1   10.049  0.001846
## Happiness$Family.new:Happiness$Freedom.new    0.96   1    1.429  0.233806
## Residuals                                   101.30 151                   
##                                               
## (Intercept)                                ***
## Happiness$Family.new                       ***
## Happiness$Freedom.new                      ** 
## Happiness$Family.new:Happiness$Freedom.new    
## Residuals                                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

\[partielles.eta^2 = \frac{\mathrm{QS}_\mathrm{Effekt}}{\mathrm{QS}_\mathrm{Effekt}+\mathrm{QS}_\mathrm{Fehler}} = \frac{0{,}96}{0{,}96 + 101{,}30} \approx 0{,}009\]

Alternativ kann auch wieder die eta_sq Funktion mit dem Zusatzargument partial = TRUE verwendet werden.

eta_sq(MANOVA, partial = TRUE)

##                                         term partial.etasq
## 1                       Happiness$Family.new         0.464
## 2                      Happiness$Freedom.new         0.067
## 3 Happiness$Family.new:Happiness$Freedom.new         0.009

Da die Effektgröße eta² dazu neigt, immer etwas zu groß auszufallen, ist es daher sinnvoll, das Konfidenzintervall für den durch den Faktor erklärten Varianzanteil zu berechnen. Für die Funktion ci.pvaf ist dabei der F-Wert, die Zählerfreiheitsgrade, die Nennerfreiheitsgrade sowie die Stichprobengröße notwendig. Diese Werte können erneut der Varianzanalysetabelle und den durchgeführten describeBy-Befehlen entnommen werden.

Anova(MANOVA, type=3)

## Anova Table (Type III tests)
## 
## Response: Happiness$Happiness.Score
##                                             Sum Sq  Df  F value    Pr(>F)
## (Intercept)                                2145.67   1 3198.336 < 2.2e-16
## Happiness$Family.new                         35.48   1   52.888 1.781e-11
## Happiness$Freedom.new                         6.74   1   10.049  0.001846
## Happiness$Family.new:Happiness$Freedom.new    0.96   1    1.429  0.233806
## Residuals                                   101.30 151                   
##                                               
## (Intercept)                                ***
## Happiness$Family.new                       ***
## Happiness$Freedom.new                      ** 
## Happiness$Family.new:Happiness$Freedom.new    
## Residuals                                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

sum(desc.Hauptfaktor1$n)

## [1] 155

Im Falle des Haupteffekts für Family.new erhält man folgendes Ergebnis.

ci.pvaf(F.value = 52.888, df.1 = 1, df.2 = 151, N=155)

## $Lower.Limit.Proportion.of.Variance.Accounted.for
## [1] 0.1455151
## 
## $Probability.Less.Lower.Limit
## [1] 0.025
## 
## $Upper.Limit.Proportion.of.Variance.Accounted.for
## [1] 0.3624183
## 
## $Probability.Greater.Upper.Limit
## [1] 0.025
## 
## $Actual.Coverage
## [1] 0.95

Das untere Limit liegt bei 14,55% erklärten Varianzanteil und das obere Limit bei 36,24%.

8 Conclusion

In diesem Post wurde die Funktionsweise der zweifaktoriellen Varianzanalyse dargelegt. Es wurden auf die Unterschiede zur ANOVA eingegangen sowie auf die graphische Darstellung von Haupt- und Interaktionseffekte.

Source

Luhmann, M. (2011). R für Einsteiger.