Table of Content

1 Introduction
2 Preparation
3 Essential requirements
3.1 Normal distribution
3.2 Sampling size
3.3 Homogeneity of variance
4 ANOVA with variance homogeneity
5 ANOVA with variance inequality
6 Post-hoc-method
7 Effect size
7.1 Effect size for ANOVA with variance homogeneity
7.2 Effect size for ANOVA with variance inequality
7.3 Calculation of Cohens f
8 Power
9 Outliers
10 Conclusion

1 Introduction

Im letzten Post “t-Test” ging es hauptsächlich um die Funktionsweise eines t-Tests für unabhängigen Stichproben. Die einfaktorielle Varianzanalyse ohne Messwiederholung kann als eine Erweiterung des t-Tests für unabhängigen Stichproben angesehen werden, da die unabhängige Variable nicht mehr dichotom sein muss. Sie kann nun auch mehr als zwei Ausprägungen haben. Für diesen Post wurde der Datensatz countries of the world von der Statsistik Plattform Kaggle https://www.kaggle.com verwendet. Eine Kopie des Datensatzes ist unter https://drive.google.com/open?id=1QO_t4hySiqVsSDsVOsKZEOHOkLlWO006 abrufbar.

library(tidyverse)
library(nortest)
library(psych)
library(car)
library(sjstats)
library(pwr)
library(ggpubr)

countries <- read_csv("countries of the world.csv")

2 Preparation

Wie auch beim t-Test wird der Datensatz countries of the world für die exemplarische Durchführung der ANOVA zunächst aufbereitet. Da die ANOVA Mittelwerte von mehr als zwei Gruppen vergleicht, werden drei neue Regionen aus der Variablen Region kreiert, sowie die abhängigen Variablen Population und Coastline als nummerische Variablen abgespeichert.

table(countries$Region)

## 
## ASIA (EX. NEAR EAST)              BALTICS  C.W. OF IND. STATES 
##                   28                    3                   12 
##       EASTERN EUROPE  LATIN AMER. & CARIB            NEAR EAST 
##                   12                   45                   16 
##      NORTHERN AFRICA     NORTHERN AMERICA              OCEANIA 
##                    6                    5                   21 
##   SUB-SAHARAN AFRICA       WESTERN EUROPE 
##                   51                   28

preparation<- countries %>% filter(Region == "LATIN AMER. & CARIB" | Region == "SUB-SAHARAN AFRICA" | Region == "ASIA (EX. NEAR EAST)" | Region == "NEAR EAST") %>%
  select(Country, Region, `Coastline (coast/area ratio)`, Population)

preparation$Population.num <- as.numeric(preparation$Population)
preparation$Coastline.new <- str_replace(preparation$`Coastline (coast/area ratio)`, ",", ".")
preparation$Coastline.num <- as.numeric(preparation$Coastline.new)
summary(preparation)

##    Country             Region          Coastline (coast/area ratio)
##  Length:140         Length:140         Length:140                  
##  Class :character   Class :character   Class :character            
##  Mode  :character   Mode  :character   Mode  :character            
##                                                                    
##                                                                    
##                                                                    
##    Population        Population.num      Coastline.new     
##  Min.   :7.502e+03   Min.   :7.502e+03   Length:140        
##  1st Qu.:7.868e+05   1st Qu.:7.868e+05   Class :character  
##  Median :6.179e+06   Median :6.179e+06   Mode  :character  
##  Mean   :3.710e+07   Mean   :3.710e+07                     
##  3rd Qu.:2.169e+07   3rd Qu.:2.169e+07                     
##  Max.   :1.314e+09   Max.   :1.314e+09                     
##  Coastline.num     
##  Min.   :  0.0000  
##  1st Qu.:  0.1075  
##  Median :  0.7050  
##  Mean   : 10.9911  
##  3rd Qu.:  7.2625  
##  Max.   :214.6700

preparation$region.new <- ifelse(preparation$Region == "SUB-SAHARAN AFRICA", "AFRICA", ifelse(preparation$Region == "LATIN AMER. & CARIB", "LATIN AMER", "Asia"))

levels(as.factor(preparation$region.new))

## [1] "AFRICA"     "Asia"       "LATIN AMER"

3 Essential requirements

Wie bei einem t-Test müssen auch für die Durchführung einer ANOVA gewisse Voraussetzungen überprüft werden:

Unabhängigkeit der Messungen. Kein Teilnehmer aus einer Gruppe darf auch in einer anderen Gruppe vorkommen.
Die abhängige Variable ist metrisch skaliert.
Die unabhängige Variable ist unabhängig und nominalskaliert.
Normalverteilung der abhängigen Variablen in allen Populationen, wenn gilt N < 30 in jeder Population.
Varianzhomogenität der abhängigen Variablen in allen Populationen.

3.1 Normal distribution

Für die Überprüfung der Normalverteilung wird der Lilliefors-Test angewendet.

lillie.test(preparation$Coastline.num)

## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  preparation$Coastline.num
## D = 0.3443, p-value < 2.2e-16

Da p < .001 liegt keine Normalverteilung der Variable Coastline vor.

3.2 Sampling size

size <- describeBy(preparation$Coastline.num, preparation$region.new, mat = TRUE)
size

##     item     group1 vars  n      mean       sd median   trimmed      mad
## X11    1     AFRICA    1 51  5.106078 16.96183   0.13  1.036585 0.192738
## X12    2       Asia    1 44 12.717955 39.40667   1.18  2.875556 1.742055
## X13    3 LATIN AMER    1 45 15.972222 21.52437   3.37 12.293243 4.862928
##     min    max  range     skew  kurtosis       se
## X11   0 107.91 107.91 4.748483 24.436128 2.375132
## X12   0 214.67 214.67 3.987602 15.779160 5.940779
## X13   0  90.47  90.47 1.447746  1.582381 3.208663

size$n

## [1] 51 44 45

Da alle Gruppen n > 30 besitzen, greift der zentrale Grenzwertsatz. Die ANOVA könnte demnach unter der Voraussetzung von Varianzhomogenität durchgeführt werden.

3.3 Homogeneity of variance

round(tapply(preparation$Coastline.num, preparation$region.new, var, na.rm=TRUE), 2)

##     AFRICA       Asia LATIN AMER 
##     287.70    1552.89     463.30

leveneTest(preparation$Coastline.num ~ preparation$region.new)

## Warning in leveneTest.default(y = y, group = group, ...): group coerced to
## factor.

## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value Pr(>F)
## group   2   1.846 0.1618
##       137

Da nun auch Varianzhomogenität (p > .05) nachgewiesen wurde, wird im nachfolgenden Schritt die Varianzanalyse durchgeführt.

4 ANOVA with variance homogeneity

Nun wird überprüft ob die Regionen “AFRICA”, “Asia” und “LATIN AMER” sich signifikant in ihrem Küstenanteil unterscheiden. Wir speichern die aov Funktion unter dem Objekt “ANOVA” ab.

ANOVA <- aov(preparation$Coastline.num ~ preparation$region.new)

Mit der model.tables Funktion und dem Zusatzargument “means” lassen sich die Mittelwerte pro Gruppe ausgeben.

model.tables(ANOVA, "means")

## Tables of means
## Grand mean
##          
## 10.99107 
## 
##  preparation$region.new 
##     AFRICA  Asia LATIN AMER
##      5.106 12.72      15.97
## rep 51.000 44.00      45.00

Der Mittelwert über alle Gruppen hinweg wird unter Grand mean angezeigt. Die zweite Zeile (rep) gibt Auskunft über die jeweilige Gruppengröße.

Für die Ausgabe der Standardabweichung (welche immer zu Mittelwertsangaben dazu genannt werden sollte) wird die describeBy Funktion verwendet.

describeBy(preparation$Coastline.num, preparation$region.new, mat = TRUE)

##     item     group1 vars  n      mean       sd median   trimmed      mad
## X11    1     AFRICA    1 51  5.106078 16.96183   0.13  1.036585 0.192738
## X12    2       Asia    1 44 12.717955 39.40667   1.18  2.875556 1.742055
## X13    3 LATIN AMER    1 45 15.972222 21.52437   3.37 12.293243 4.862928
##     min    max  range     skew  kurtosis       se
## X11   0 107.91 107.91 4.748483 24.436128 2.375132
## X12   0 214.67 214.67 3.987602 15.779160 5.940779
## X13   0  90.47  90.47 1.447746  1.582381 3.208663

Um das Ergebniss der Varianzanalyse zu erhalten, wird die summary Funktion auf das Objekt “ANOVA” angewendet.

summary(ANOVA)

##                         Df Sum Sq Mean Sq F value Pr(>F)
## preparation$region.new   2   3014  1507.0   2.033  0.135
## Residuals              137 101544   741.2

Das Ergebnis besteht aus zwei Zeilen. Zeile 1 enthält die Angaben zum Effekt des Faktors region.new (beziehungsweise zwischen den Gruppen). Zeile 2 steht mit Residuals für Rest und bezieht sich auf den Anteil der Varianz des Fehlers (beziehungsweise innerhalb der Gruppen).

Df Die Freiheitsgrade des F -Werts.

Sum Sq Die Quadratsummen zwischen den Gruppen (Zeile 1) und innerhalb der Gruppen (Zeile 2).

Mean Sq Die mittleren Quadratsummen. Diese werden gebildet, indem man die Quadratsummen durch die jeweiligen Freiheitsgrade teilt.

F value Die empirische Prüfgröße F. Sie wird berechnet, indem man die mittleren Quadratsummen zwischen den Gruppen (Zeile 1) durch die mittleren Quadratsummen innerhalb der Gruppen (Zeile 2) dividiert.

Pr(>F) Der p-Wert für die Varianzanalyse. Er steht für die Wahrscheinlichkeit, diesen oder einen größeren F-Wert zu finden, wenn die Nullhypothese gilt.

Das Ergebnis ist mit p = .135 nicht signifikant. Es gibt also erstmal keinen Unterschied zwischen den Regionen hinsichtlich ihres Küstenanteils.

5 ANOVA with variance inequality

Es kann auch bei einer Varianzanalyse vorkommen, dass die Varianzen der abhängigen Variablen in einer Population nicht gleich verteilt ist. Im Nachfolgenden wollen wir überprüfen, ob die Regionen “AFRICA”, “Asia” und “LATIN AMER” sich signifikant in ihrem Populationsanteil unterscheiden.

Überprüfung der Normalverteilung

lillie.test(preparation$Population.num)

## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  preparation$Population.num
## D = 0.40017, p-value < 2.2e-16

Wir sehen, dass die Variable Population.num nicht normalverteilt ist. Nun wird erneut die Stichprobengröße der beiden Gruppen betrachtet.

Stichprobengröße

size2 <- describeBy(preparation$Population.num, preparation$region.new, mat = TRUE)
size2$n

## [1] 51 44 45

In allen Populationen gilt n > 30. Es greift erneut der zentrale Grenzwertsatz.

Überprüfung der Varianzhomogenität

leveneTest(preparation$Population.num ~ preparation$region.new)

## Warning in leveneTest.default(y = y, group = group, ...): group coerced to
## factor.

## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value Pr(>F)  
## group   2  3.9397 0.0217 *
##       137                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Wir erhalten ein signifikantes Ergebnis. Dies bedeutet, dass Varianzungleichheit vorliegt. Anstelle der ANOVA wird daher der oneway.test (Welch) durchgeführt.

One-way-Test (Welch) bei Varianzungleichheit

oneway.test(preparation$Population.num ~ preparation$region.new)

## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  preparation$Population.num and preparation$region.new
## F = 1.9421, num df = 2.000, denom df = 74.368, p-value = 0.1506

Das Ergebnis ist mit p = .151 nicht signifikant. Es gibt also keinen Unterschied zwischen den Regionen hinsichtlich ihres Populationsanteils.

6 Post-hoc-method

Ein signifikantes / nicht signifikantes Ergebnis besagt lediglich, dass es allgemein Mittelwertsunterschiede / keine Mittelwertsunterschiede in dem Test gibt. Wir wissen jedoch nicht, um welche Mittelwerte es sich handelt. Um dies aufzuklären werden im kommenden Schritt alle Mittelwerte paarweise mit t-Tests für unabhängige Stichproben verglichen. Um die alpha-Fehler Kumulierung zu verhindern, wird eine alpha-Fehler Adjustierung durchgeführt. Für die einfaktorielle Varianzanalyse ohne Messwiederholung bietet sich die Bonferroni-Korrektur an. Sie wird mithilfe der pairwise.t.test Funktion angefordert.

pairwise.t.test(preparation$Population.num, preparation$region.new, p.adj= "bonferroni")

## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  preparation$Population.num and preparation$region.new 
## 
##            AFRICA Asia 
## Asia       0.042  -    
## LATIN AMER 1.000  0.042
## 
## P value adjustment method: bonferroni

Wir sehen, dass es weder bei den Gruppen “AFRICA” und “Asia” noch bei den Gruppen “Asia” und “LATIN AMER” einen signifikanten Unterschied gibt.

7 Effect size

Eine sehr beliebte Effektgröße für die einfaktorielle Varianzanalyse ohne Messwiederholung ist das eta².

7.1 Effect size for ANOVA with variance homogeneity

Das eta² wird folgendermaßen berechnet: \[\eta^2 = \frac{\mathrm{QS}_\mathrm{Zwischen}}{\mathrm{QS}_\mathrm{Gesamt}}\]

QS steht für Quadratsummen. Diese Werte können wir der Varianzanalysetabelle entnommen werden.

summary(ANOVA)

##                         Df Sum Sq Mean Sq F value Pr(>F)
## preparation$region.new   2   3014  1507.0   2.033  0.135
## Residuals              137 101544   741.2

\[\eta^2 = \frac{\mathrm{QS}_\mathrm{Zwischen}}{\mathrm{QS}_\mathrm{Gesamt}} = \frac{3014}{101544} \approx 0{,}029\]

Alternativ kann man auch die eta_sq Funktion verwenden.

eta_sq(ANOVA)

##                     term etasq
## 1 preparation$region.new 0.029

7.2 Effect size for ANOVA with variance inequality

Schwieriger wird die Bestimmung der Effektgröße, wenn man mangels Varianzhomogenität gezwungen war den oneway.test nach Welch durchzuführen. Hier nochmal das Ergebnis des Tests (5 ANOVA with variance inequality/One-way-Test (Welch) bei Varianzungleichheit).

oneway.test(preparation$Population.num ~ preparation$region.new)

## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  preparation$Population.num and preparation$region.new
## F = 1.9421, num df = 2.000, denom df = 74.368, p-value = 0.1506

Hier haben wir keine Quadratsummen angegeben, mit denen wir die Effektgröße berechnen könnten. Auch die eta_sq Funktion kann hier nicht angewendet werden, da diese nur bei aov-Modellen funktioniert. Mit ein wenig Aufwand, lassen sich die Quadratsummen und letztendlich die Effektstärke trotzdem berechnen.

m.i <- tapply(preparation$Population.num, preparation$region.new, mean)
v.i <- tapply(preparation$Population.num, preparation$region.new, var)
n.i <- tapply(preparation$Population.num, preparation$region.new, length)

SS_within <- sum((n.i-1) * v.i)
SS_between <- sum(n.i * (m.i - mean(preparation$Population.num))^2)
SS_total <- (length(preparation$Population.num)-1) * var(preparation$Population.num)
SS_between/SS_total

## [1] 0.0561803

7.3 Calculation of Cohens f

Aus dem eta² kann nun die Effektgröße f nach Cohen berechnet werden. Im ersten Schritt weisen wir dazu das eta² aus der durchgeführten ANOVA dem Objekt “f.ANOVA” zu.

f.ANOVA <- eta_sq(ANOVA)

Die Formel für Cohens f sieht in R folgendermaßen aus.

f.1 <- sqrt(as.numeric(f.ANOVA)/(1-as.numeric(f.ANOVA)))
f.1

## [1]        NA 0.1722846

Alternativ bestünde die Möglicheit, die cohens_f Funktion zu verwenden. Diese funktioniert allerdings nur wie die eta_sq Funktion bei aov-Modelle.

cohens_f(ANOVA)

##                     term  cohens.f
## 1 preparation$region.new 0.1722846

Das selbe wird nun auch für den oneway.test durchgeführt.

f.oneway.test <- SS_between/SS_total
f.2 <- sqrt(as.numeric(f.oneway.test)/(1-as.numeric(f.oneway.test)))
f.2

## [1] 0.2439762

Wir erhalten für die ANOVA einen f-Wert von 0,17 und für den oneway.test einen f-Wert von 0,24. Warum haben wir zusätzlich ein weiteres Maß der Effektgröße berechnet, nachdem wir bereits eta² hatten?

8 Power

Die Frage, warum zusätzlich Cohens f berechnet wurde, klärt sich, wenn die Teststärke berechnet werden soll. Im Nachfolgenden soll eine Power Analyse für die ANOVA (4 ANOVA with variance homogeneity) durchgeführt werden. Für die pwr.anova.test Funktion werden folgende Parameter benötigt:

k = Anzahl der Gruppen
f = Cohens f
sig.level = das Signifikanzniveau
n = Gruppengröße (der kleinsten Gruppe)

Für die zu analysierende ANOVA ergibt dies fogende Syntax.

pwr.anova.test(k=3, f = 0.1722846, sig.level = 0.135, n= 44)

## 
##      Balanced one-way analysis of variance power calculation 
## 
##               k = 3
##               n = 44
##               f = 0.1722846
##       sig.level = 0.135
##           power = 0.5901031
## 
## NOTE: n is number in each group

Die ANOVA besitzt eine Teststärke von 0,59. Gewünscht wäre eine Stärke von 0,8. Im Nachgang wird nun berechnet, wie viele Personen man pro Gruppe für die ANOVA bräuchte, um folgende Werte zu erhalten:

k = 3
f = 0,25
sig.level = 0,05
power = 0,8

pwr.anova.test(k=3, f = 0.25, sig.level = 0.05, power = 0.80)

## 
##      Balanced one-way analysis of variance power calculation 
## 
##               k = 3
##               n = 52.3966
##               f = 0.25
##       sig.level = 0.05
##           power = 0.8
## 
## NOTE: n is number in each group

Um eine Teststärke von 0,8 bei einem Signifikanzlevel von 0,05 und einer Effektgröße von 0,25 zu bekommen, bedarf es einer Gruppengröße von mindestens 53 in allen Gruppen. Die Größe der gesamten Stichprobe (für die angegebenen Parameter) lässt sich folgendermaßen berechnen.

pwr.anova.test(k=3, f = 0.25, sig.level = 0.05, power = 0.80)$n * pwr.anova.test(k=3, f = 0.25, sig.level = 0.05, power = 0.80)$k

## [1] 157.1898

Es sind insgesamt 158 Observations notwendig.

9 Outliers

Zu einer ANOVA ist ein Boxplot Diagramm immer sehr nützlich, da es viel über die Verteilung der abhängigen Variablen aussagt und etwaige Ausreißer schnell identifiziert werden könne.

ggboxplot(preparation, x = "region.new", y = "Coastline.num", 
          color = "region.new", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
          order = c("AFRICA", "Asia", "LATIN AMER"),
          ylab = "Coastline", xlab = "Region")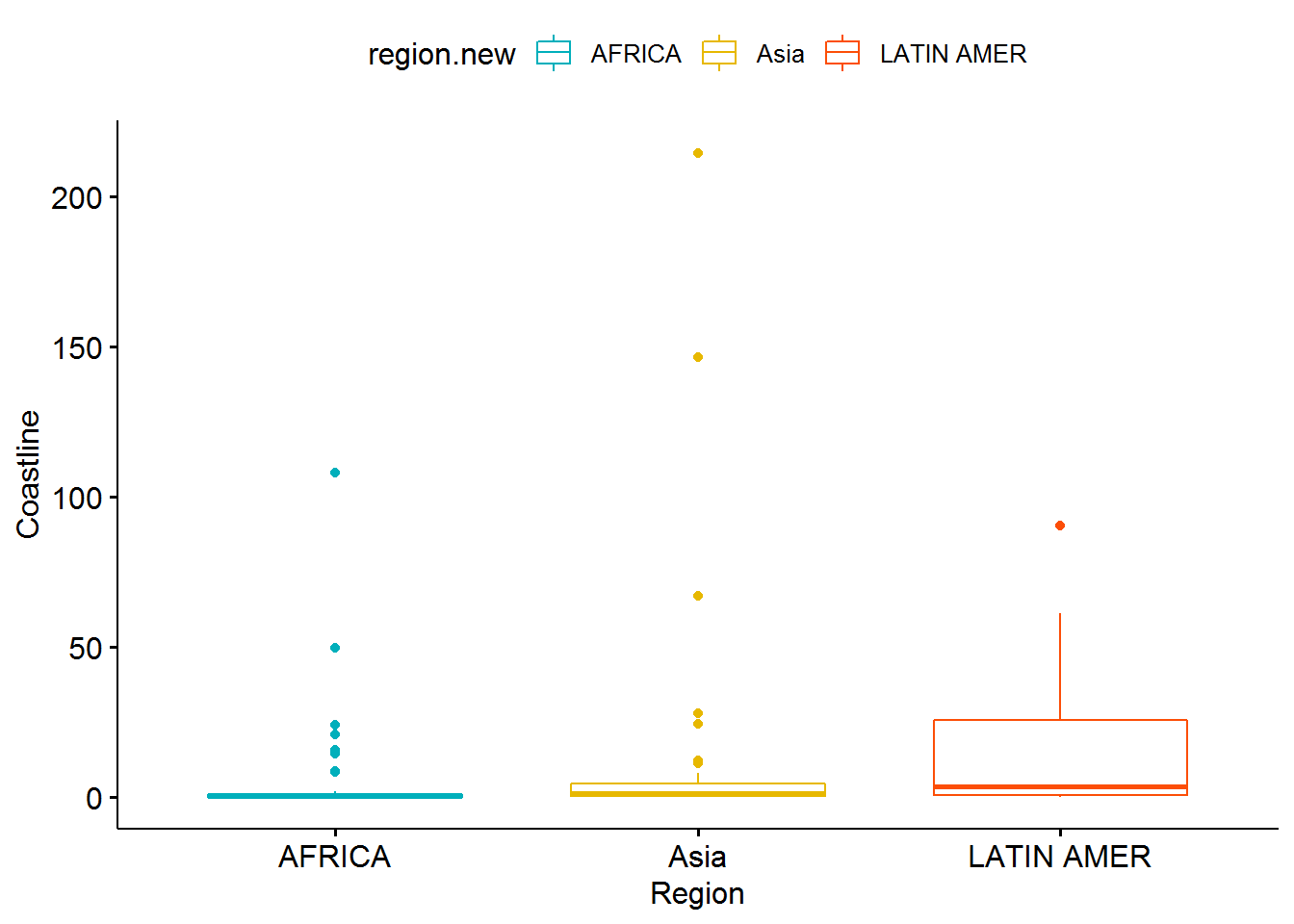

Wie wir sehen können, sind mehrere Ausreißer vorhanden. Nun stellt sich die Frage, ob dies eine Auswirkung auf die durchgeführten Signifikanztests hatte.

describe(preparation$Coastline.num)

##    vars   n  mean    sd median trimmed  mad min    max  range skew
## X1    1 140 10.99 27.43    0.7    4.37 1.05   0 214.67 214.67 4.49
##    kurtosis   se
## X1    25.01 2.32

Die describe Funktion zeigt, dass der Mittelwert bei 10,99 liegt mit einer Standardabweichung von 27,43. Wir schmeißen nun alle Werte größer 70 mit dem filter Befehl raus.

without.outliers<- preparation %>% filter(Coastline.num < 70)

leveneTest(without.outliers$Coastline.num ~ as.factor(without.outliers$region.new))

## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value    Pr(>F)    
## group   2  9.2706 0.0001702 ***
##       133                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Der levene Test zeigt nun ein signifikantes Ergebnis. Es liegt Varianzheterogenität vor. Demnach darf die ANOVA nicht verwendet werden. Wir greifen daher auf den oneway.test (Welch) zurück.

oneway.test(without.outliers$Coastline.num ~ without.outliers$region.new)

## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  without.outliers$Coastline.num and without.outliers$region.new
## F = 6.7628, num df = 2.000, denom df = 78.374, p-value = 0.001952

Wir sehen, wenn wir die Outlier nicht weiter berücksichtigen, gibt es doch einen signifikanten Unterschied zwischen den Regionen hinsichtlich ihres Küstenanteils.

10 Conclusion

Wie wir im letzten Abschnitt gesehen haben, ist es zwingend notwendig nicht nur die Voraussetzungen für die statistischen Tests zu beachten, sondern auch die Verteilung der Variablen. Dies kann im Zweifel einen erheblichen Unterschied bei den Ergebnissen und den daraus gezogenen Schlussfolgerungen machen.

Source

Luhmann, M. (2011). R für Einsteiger.