Table of Content

1 Introduction
2 Contingency table
2.1 Absolute Frequency
2.2 Relative Frequency
2.3 Multidimensional contingency tables
3.1 Pearsons correlation
3.2 Covariance
4 Correlations for non-metric variables
4.1 metric - ordinal
4.2 ordinal - ordinal
5 Conclusion

1 Introduction

Aufbauend auf dem vorangegangenen Post “Univariate descriptive statistics” wird im folgenden Beitrag die gleichzeitige Betrachtung von zwei Variablen thematisiert. Für diesen Post werden die Datensätze insurance und Automobile_data von der Statsistik Plattform Kaggle https://www.kaggle.com verwendet. Eine Kopie der Datensätze ist unter https://drive.google.com/open?id=1_fK9j74lRidUOsC_tlCAYbaJLuWzgR-e (insurance) und https://drive.google.com/open?id=103HRmDLEkGnIizFzIlpErv1uYHiw1DmT (Automobile_data) abrufbar.

library("tidyverse")
library("psych")

insurance <- read_csv("insurance.csv")
Automobile_data <- read_csv("Automobile_data.csv")

2 Contingency table

In Kontingenztabellen wird die Häufigkeit für jede mögliche Kombination mehrerer Variablen angegeben. Im Nachfolgenden werden absolute und relative Häufigkeiten sowie mehrdimensionale Kontingenztabellen anhand des Datensatzes insurance vorgestellt.

glimpse(insurance)

## Observations: 1,338
## Variables: 7
## $ age      <int> 19, 18, 28, 33, 32, 31, 46, 37, 37, 60, 25, 62, 23, 5...
## $ sex      <chr> "female", "male", "male", "male", "male", "female", "...
## $ bmi      <dbl> 27.900, 33.770, 33.000, 22.705, 28.880, 25.740, 33.44...
## $ children <int> 0, 1, 3, 0, 0, 0, 1, 3, 2, 0, 0, 0, 0, 0, 0, 1, 1, 0,...
## $ smoker   <chr> "yes", "no", "no", "no", "no", "no", "no", "no", "no"...
## $ region   <chr> "southwest", "southeast", "southeast", "northwest", "...
## $ charges  <dbl> 16884.924, 1725.552, 4449.462, 21984.471, 3866.855, 3...

2.1 Absolute Frequency

Eindimensionale absolute Häufigkeitstabellen wurden bereits im Post “Univariate descriptive statistics” unter Punkt 2.1 beschrieben. Die table Funktion kann allerdings auch auf zwei Variablen angewandt werden.

table(insurance$smoker, insurance$sex)

##      
##       female male
##   no     547  517
##   yes    115  159

Wir sehen die absoluten Häufigkeiten für Raucher / Nichtraucher aufgeteilt nach Geschlecht. Darüber hinaus kann man in R mit dem Befehl addmargins die Zeilen- und Spaltensummen sowie die Gesamthäufigkeit anfordern.

addmargins(table(insurance$smoker, insurance$sex))

##      
##       female male  Sum
##   no     547  517 1064
##   yes    115  159  274
##   Sum    662  676 1338

2.2 Relative Frequency

Im Gegensatz zu Häufigkeitstabellen (“Univariate descriptive statistics” Abschnitt 2.2) kommt bei Kontingenztabellen noch eine Besonderheit hinzu. Je nachdem welchen Wert man als Referenz nimmt, hat man die Auswahl zwischen mehreren verschiedenen relativen Häufigkeiten: + Gesamthäufigkeit + Zeilensumme + Spaltensumme

Relative Häufigkeiten in Bezug zur Gesamthäufigkeit

Diese erhählt man wie gewohnt mit der prop.table Funktion.

prop.table(table(insurance$smoker, insurance$sex))

##      
##           female       male
##   no  0.40881913 0.38639761
##   yes 0.08594918 0.11883408

Die relative Zeilen- uns Spaltenhäufigkeit sowie die relative Gesamthäufigkeit erhält man mit dem Befehl addmargins.

addmargins(prop.table(table(insurance$smoker, insurance$sex)))

##      
##           female       male        Sum
##   no  0.40881913 0.38639761 0.79521674
##   yes 0.08594918 0.11883408 0.20478326
##   Sum 0.49476831 0.50523169 1.00000000

Relative Häufigkeiten in Bezug zur Zeilensumme

Um den Bezug zur Zeilensumme anzufordern, wird der Befehl um das Argument 1 erweitert.

prop.table(table(insurance$smoker, insurance$sex), 1)

##      
##          female      male
##   no  0.5140977 0.4859023
##   yes 0.4197080 0.5802920

Relative Häufigkeiten in Bezug zur Spaltensumme

Für den Bezug zur Spaltensumme, muss der Befehl mit dem Zusatzargument 2 ergänzt werden.

prop.table(table(insurance$smoker, insurance$sex), 2)

##      
##          female      male
##   no  0.8262840 0.7647929
##   yes 0.1737160 0.2352071

2.3 Multidimensional contingency tables

In R besteht auch die Möglichkeit, drei oder mehr Variablen in Kontingenztabellen miteinander zu kombinieren. In der Regel teilt R mehrdimensionale Kontingenztabellen in mehrere zweidimensionale Tabellen auf.

table(insurance$smoker, insurance$region, insurance$sex)

## , ,  = female
## 
##      
##       northeast northwest southeast southwest
##   no        132       135       139       141
##   yes        29        29        36        21
## 
## , ,  = male
## 
##      
##       northeast northwest southeast southwest
##   no        125       132       134       126
##   yes        38        29        55        37

3 Correlations for metric variables

Der Zusammenhang zwischen metrischen Variablen kann über die Produkt-Moment-Korrelation (Pearson) oder über die Kovarianz bestimmt werden. Die nachfolgenden Befehle beziehen sich auf die Variablen aus dem Datensatz Automobile_data.

glimpse(Automobile_data)

## Observations: 205
## Variables: 26
## $ symboling           <int> 3, 3, 1, 2, 2, 2, 1, 1, 1, 0, 2, 0, 0, 0, ...
## $ `normalized-losses` <chr> "?", "?", "?", "164", "164", "?", "158", "...
## $ make                <chr> "alfa-romero", "alfa-romero", "alfa-romero...
## $ `fuel-type`         <chr> "gas", "gas", "gas", "gas", "gas", "gas", ...
## $ aspiration          <chr> "std", "std", "std", "std", "std", "std", ...
## $ `num-of-doors`      <chr> "two", "two", "two", "four", "four", "two"...
## $ `body-style`        <chr> "convertible", "convertible", "hatchback",...
## $ `drive-wheels`      <chr> "rwd", "rwd", "rwd", "fwd", "4wd", "fwd", ...
## $ `engine-location`   <chr> "front", "front", "front", "front", "front...
## $ `wheel-base`        <dbl> 88.6, 88.6, 94.5, 99.8, 99.4, 99.8, 105.8,...
## $ length              <dbl> 168.8, 168.8, 171.2, 176.6, 176.6, 177.3, ...
## $ width               <dbl> 64.1, 64.1, 65.5, 66.2, 66.4, 66.3, 71.4, ...
## $ height              <dbl> 48.8, 48.8, 52.4, 54.3, 54.3, 53.1, 55.7, ...
## $ `curb-weight`       <int> 2548, 2548, 2823, 2337, 2824, 2507, 2844, ...
## $ `engine-type`       <chr> "dohc", "dohc", "ohcv", "ohc", "ohc", "ohc...
## $ `num-of-cylinders`  <chr> "four", "four", "six", "four", "five", "fi...
## $ `engine-size`       <int> 130, 130, 152, 109, 136, 136, 136, 136, 13...
## $ `fuel-system`       <chr> "mpfi", "mpfi", "mpfi", "mpfi", "mpfi", "m...
## $ bore                <chr> "3.47", "3.47", "2.68", "3.19", "3.19", "3...
## $ stroke              <chr> "2.68", "2.68", "3.47", "3.4", "3.4", "3.4...
## $ `compression-ratio` <dbl> 9.00, 9.00, 9.00, 10.00, 8.00, 8.50, 8.50,...
## $ horsepower          <chr> "111", "111", "154", "102", "115", "110", ...
## $ `peak-rpm`          <chr> "5000", "5000", "5000", "5500", "5500", "5...
## $ `city-mpg`          <int> 21, 21, 19, 24, 18, 19, 19, 19, 17, 16, 23...
## $ `highway-mpg`       <int> 27, 27, 26, 30, 22, 25, 25, 25, 20, 22, 29...
## $ price               <chr> "13495", "16500", "16500", "13950", "17450...

3.1 Pearsons correlation

Im folgenden Abschnitt sollen drei Möglichkeiten, die Pearson Korrelation anzufordern, vorgestellt werden:

cor - Funktion
cor.test - Funktion
corr.test - Funktion

cor-Funktion

Die Korrelation zwischen zwei oder mehreren Variablen wird mit der cor Funktion angefordert. In unserem Beispieldatensatz werden dafür die beiden Variablen horsepower und price in metrische Variablen umgewandelt (warum auch immer sie als character abgespeichert waren) und mit der Variablen ´curb-weight´ in den neuen data.frame “Korrelation” abgespeichert. Darauf wird nun die cor Funktion angewandt.

Automobile_data$Power <- as.numeric(Automobile_data$horsepower)

## Warning: NAs durch Umwandlung erzeugt

Automobile_data$Car_Price <- as.numeric(Automobile_data$price)

## Warning: NAs durch Umwandlung erzeugt

Korrelation <- data.frame(Automobile_data$Power, Automobile_data$Car_Price, Automobile_data$`curb-weight`)
cor(Korrelation)

##                               Automobile_data.Power
## Automobile_data.Power                             1
## Automobile_data.Car_Price                        NA
## Automobile_data..curb.weight.                    NA
##                               Automobile_data.Car_Price
## Automobile_data.Power                                NA
## Automobile_data.Car_Price                             1
## Automobile_data..curb.weight.                        NA
##                               Automobile_data..curb.weight.
## Automobile_data.Power                                    NA
## Automobile_data.Car_Price                                NA
## Automobile_data..curb.weight.                             1

Das Ergebnis ist erst einmal unübersichtlich, da die Spaltennamen zu lang ausgegeben werden. Wir benennen sie daher während der data.frame Zuweisung um.

Korrelation2 <- data.frame(Power = Automobile_data$Power, Price = Automobile_data$Car_Price, Weight = Automobile_data$`curb-weight`)
cor(Korrelation2)

##        Power Price Weight
## Power      1    NA     NA
## Price     NA     1     NA
## Weight    NA    NA      1

Schon viel besser. Aber nun besteht das Problem mit den NA’s noch. Natürlich könnte man mit der na.omit Funktion alle leeren Spalten löschen, aber dabei würde man eventuell wichtige Werte verlieren.
Bei der cor Funktion kann man stattdessen die beiden Zusatzargumente use=“pairwise” und use=“complete” verwenden.

Bei dem use=“pairwise” Argument werden alle Fälle für jede bivariate Korrelation verwendet, die gültige Werte auf diesen Variablen haben. Dies geschieht unabhängig davon, ob sie auf den anderen Variablen in der Korrelationsmatrix fehlende Werte haben. Bei dem use=“complete” Argument werden nur die Fälle berücksichtigt, die auf allen in der Korrelationsmatrix enthaltene variablen gültige Werte haben.

In unserem Beispiel verwenden wir die complete-Variante.

cor(Korrelation2, use = "complete")

##            Power     Price    Weight
## Power  1.0000000 0.8105331 0.7580625
## Price  0.8105331 1.0000000 0.8350904
## Weight 0.7580625 0.8350904 1.0000000

Zusammenhangsmaße lassen sich auch prima plotten.

plot(Korrelation2)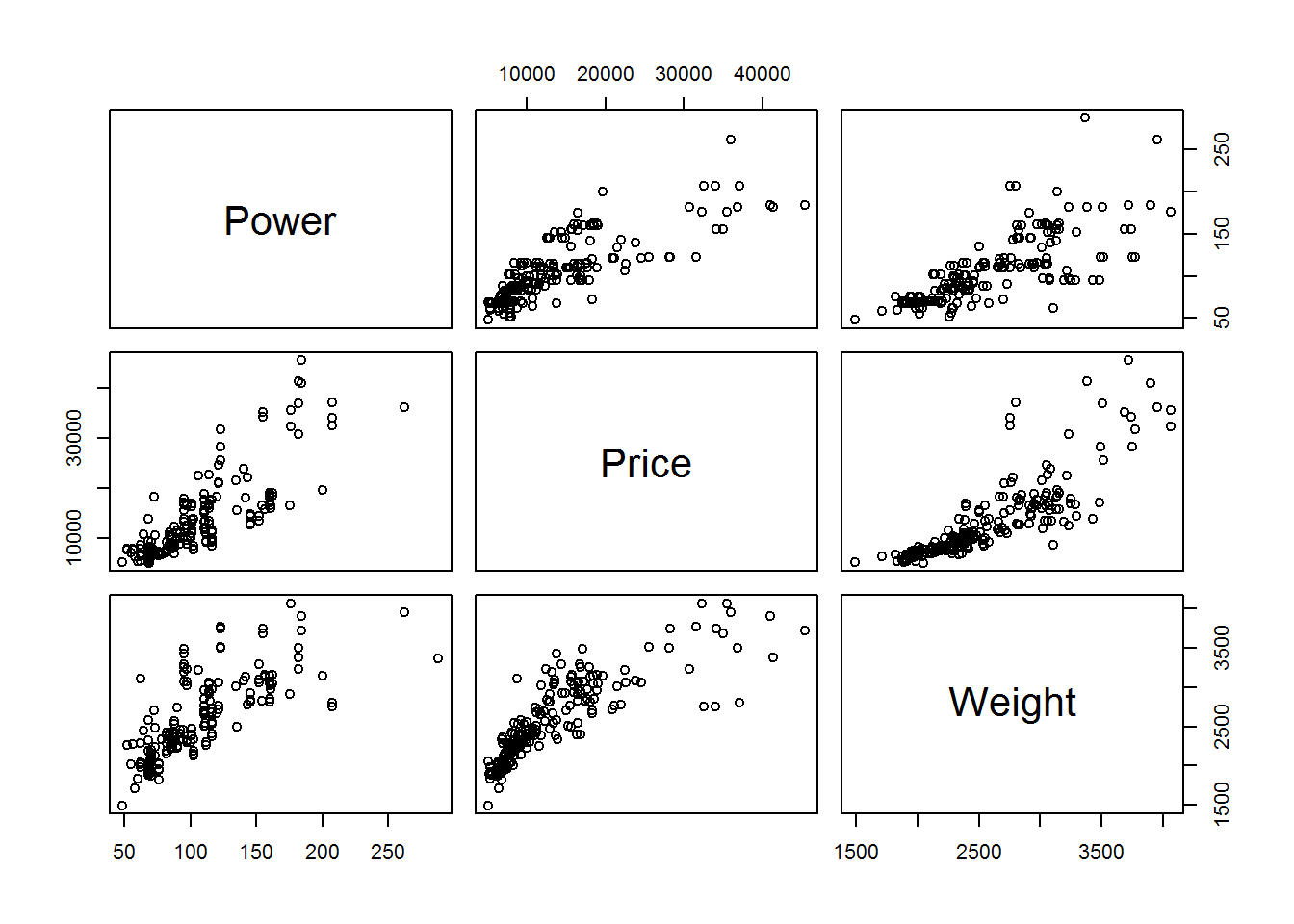

corr.test-Funktion

Als Ergänzung zu der cor Funktion kann die corr.test Funktion angefordert werden. Mit ihr erhalten wir weitere statistische Angaben.

corr.test(Korrelation2)

## Call:corr.test(x = Korrelation2)
## Correlation matrix 
##        Power Price Weight
## Power   1.00  0.81   0.75
## Price   0.81  1.00   0.83
## Weight  0.75  0.83   1.00
## Sample Size 
##        Power Price Weight
## Power    203   199    203
## Price    199   201    201
## Weight   203   201    205
## Probability values (Entries above the diagonal are adjusted for multiple tests.) 
##        Power Price Weight
## Power      0     0      0
## Price      0     0      0
## Weight     0     0      0
## 
##  To see confidence intervals of the correlations, print with the short=FALSE option

Die Ausgabe besteht aus drei Teilen:

Die Korrelationskoeffizienten für alle bivariaten Variablenkombinationen.
Die Anzahl der Fälle, die in die Berechnung eingeflossen sind.
Der p-Wert für den jeweiligen Korrelationskoeffizienten.

Ergänzend zum letzten Punkt: die p-Werte unterhalb der Diagonalen beruhen auf den normalen bivariaten Tests. Bei den p-Werten oberhalb der Diagonalen wurde eine Korrektur für multiple Tests durchgeführt. Die p-Werte oberhalb der Diagonalen sind daher immer größer als die p-Werte unterhalb der Diagonalen. Deutlich wird dies, wenn man die p-Werte des corr.tests explizit anfordert.

corr.test(Korrelation2)$p

##               Power        Price       Weight
## Power  0.000000e+00 2.378256e-47 4.321574e-38
## Price  1.189128e-47 0.000000e+00 6.568732e-53
## Weight 4.321574e-38 2.189577e-53 0.000000e+00

Diese Funktion kann man auch für anderweitige statistische Kennwerte anwenden:

$p = p-Werte
$t = t-Werte
$se = Standardfehler
$ci = Konfidenzintervalle

cor.test-Funktion

Die cor.test Funktion hat gegenüber der corr.test Funktion einen entscheidenden Vorteil. Mit ihr kann man auch gerichtete Hypothesen testen. Ein Nachteil ist jedoch, dass man die cor.test Funktion nur zwei Variablen anwenden kann.

cor.test(Automobile_data$Power, Automobile_data$Car_Price)

## 
##  Pearson's product-moment correlation
## 
## data:  Automobile_data$Power and Automobile_data$Car_Price
## t = 19.424, df = 197, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.7567577 0.8534119
## sample estimates:
##       cor 
## 0.8105331

An dem Satz “alternative hypothesis: true correlation is not equal to 0” erkennt man, dass in dem vorliegenden Beispiel überprüft wurde, ob der Korrelationskoeffizient ungleich Null ist. Mit den Zusatzargumenten alternative=“less” und alternative=“greater” kann geprüft werden (gerichtete Hypothesen), ob die Korrelation kleiner Null (less) ist oder in Variante 2 größer Null (greater) ist.

cor.test(Automobile_data$Power, Automobile_data$Car_Price, alternative = "greater")

## 
##  Pearson's product-moment correlation
## 
## data:  Automobile_data$Power and Automobile_data$Car_Price
## t = 19.424, df = 197, p-value < 2.2e-16
## alternative hypothesis: true correlation is greater than 0
## 95 percent confidence interval:
##  0.7662131 1.0000000
## sample estimates:
##       cor 
## 0.8105331

cor.test(Automobile_data$Power, Automobile_data$Car_Price, alternative = "less")

## 
##  Pearson's product-moment correlation
## 
## data:  Automobile_data$Power and Automobile_data$Car_Price
## t = 19.424, df = 197, p-value = 1
## alternative hypothesis: true correlation is less than 0
## 95 percent confidence interval:
##  -1.0000000  0.8471781
## sample estimates:
##       cor 
## 0.8105331

Die Stärke des Zusammenhangs (0,81) bleibt dabei gleich. Allerdings ändert sich der p-Wert (1) bei dem zweiten Test zu “nicht signifikant”, da der Zusammenhang schließlich positiv ist.

3.2 Covariance

Die Kovarianz ist ein unstandardisiertes Zusammenhangsmaß. Im Gegenzug zur Korrelation hat sie keinen festgelegten Wertebereich.

cov(Automobile_data$Power, Automobile_data$Car_Price, use = "complete")

## [1] 242860.9

Wir erhalten im Beispiel eine positive Kovarianz. Das bedeutet, dass mit ansteigender PS Zahl der Kaufpreis des Autos ansteigt. Man kann sich auch für die Kovarinz mit einer Kombination von Variablen ausgeben lassen.

cov(Korrelation2, use = "pairwise")

##             Power      Price     Weight
## Power    1577.231   242860.9   15605.57
## Price  242860.944 63155863.4 3430270.94
## Weight  15605.575  3430270.9  271107.87

So eine Matrix nennt man auch Varianz-Kovarianz Matrix, da sie sowohl die Kovarianzen der Variablenpaare als auch die Varianzen der einzelnen Variablen enthält. Die Varianzen stehen dabei in der Diagonalen. Überprüfen können wir das, wenn wir gezielt die Varianz für die Variable Power anfordern.

var(Automobile_data$Power, use = "complete")

## [1] 1577.231

4 Correlations for non-metric variables

Die Pearson Korrelation sowie die Kovarianz dürfen nur für metrische Variablen berechnet werden, da sie auf den Mittelwerten und Varianzen der Variablen basieren. Haben wir (teilweise) ein anderes Skalenniveau, müssen wir auch andere Tests durchführen.

4.1 metric - ordinal

Möchte man eine metrische Variable und eine ordinalskalierte Variable miteinander korrelieren lassen, so muss man die Korrelation nach “Spearman” durchführen. Für ein anschauliches Beispiel, ergänzen wir den Datensatz Automobile_data um eine ordinalskalierte Variable cylinders.numeric.

class(Automobile_data$`num-of-cylinders`)

## [1] "character"

table(Automobile_data$`num-of-cylinders`)

## 
##  eight   five   four    six  three twelve    two 
##      5     11    159     24      1      1      4

Automobile_data$cylinders <- recode(Automobile_data$`num-of-cylinders`, `two`="2", `four`="4", `six`="6", `eight`="8")
Automobile_data$cylinders.numeric <- as.numeric(Automobile_data$cylinders)

## Warning: NAs durch Umwandlung erzeugt

summary(Automobile_data$cylinders.numeric)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##   2.000   4.000   4.000   4.312   4.000   8.000      13

Mit dem Zusatzargument in der cor Funktion method=“spearman” führt man eine Korrelation nach Spearman durch.

cor(Automobile_data$cylinders.numeric, Automobile_data$Car_Price, use = "complete", method = "spearman")

## [1] 0.4889311

4.2 ordinal - ordinal

Möchte man zwei ordinalskalierte Variablen miteinander korrelieren lassen, so muss man die Korrelation nach “Kenall” durchführen. Dafür kreieren wir die ordinalskalierte Variable Power.grouped.num.

Automobile_data$Power.grouped <- ifelse(Automobile_data$Power >= 116, "3", ifelse(Automobile_data$Power < 70, "1", "2"))
Automobile_data$Power.grouped.num <- as.numeric(Automobile_data$Power.grouped)

Mit dem Zusatzargument method=“kendall” führt man nun eine Korrelation nach Kendall durch.

cor(Automobile_data$cylinders.numeric, Automobile_data$Power.grouped.num, use = "complete", method = "kendall")

## [1] 0.46938

5 Conclusion

In diesem Post wurden mehrere Möglichkeiten gezeigt, wie der Zusammenhang bivariater Variablen, je nach Skalenniveau, beschrieben werden kann.

Source

Luhmann, M. (2011). R für Einsteiger.

Bivariate descriptive statistics