2.1 Mean absolute deviation

Die mittlere absolute Abweichung (s) misst die durchschnittliche absolute Abweichung vom arithmetischen Mittelwert. Es wird mit absoluten Abweichungen gerechnet, da sich sonst positive und negative Differenzen gegenseitig ausgleichen würden.

Berechnung:

Nehmen wir an, eine Familie hat fünf Kinder im Alter von 1, 3, 5, 9 und 12 Jahren. Der arithmetische Mittelwert, der im ersten Schritt berechnet werden muss, ist demzufolge: \[ Mittelwert = \frac{1+3+5+9+12}{5} = 6 \]

Die mittlere absolute Abweichung ist: \[ s = \frac{|1-6|+|3-6|+|5-6|+|9-6|+|12-6|}{5} \] \[ s = \frac{(5+3+1+3+6)}{5} =3,6 \]

Die mittlere absolute Abweichung beträgt 3,6 Jahre.

2.2 Variance

Die Varianz misst die mittlere quadratische Abweichung vom arithmetischen Mittelwert.

Berechnung:

Als Beispiel nehmen wir wieder die Familie mit den fünf Kindern her. Zur Berechnung der Varianz wird wieder der arithmetische Mittelwert benötigt. Dieser war in unserem Beispiel: 6 [(1+3+5+9+12)/5].

\[ Varianz = \frac{((1-6)^2+(3-6)^2+(5-6)^2+(9-6)^2+(12-6)^2)}{5} \] \[ Varianz = \frac{(25+9+1+9+36)}{5} =16 \]

In der Formel zur Varianz werden die Abweichungen aller Werte (Alter) vom arithmetischen Mittelwert (durchschnittliches Alter) quadriert, aufsummiert und anschließend durch die Anzahl der Merkmalsträge (Kinder) geteilt.

Die Varianz ist in unserem Beispiel wenig aussagekräftig, da hier letztlich Differenzen zwischen Jahre quadriert wurden. Demzufolge ist eine Varianz von 16 bei Werten, die nur von 1 bis 12 (Jahren) reichen, schwer interpretierbar. Des Weiteren hat die Varianz den Nachteil, dass sie empfindlich gegenüber Ausreißern ist. Nehmen wir an, dass die Familie noch ein weiteres Kind mit 24 Jahren hat. Das arithmetische Mittel würde sich auf 9 erhöhen und die Varianz auf 58,33. Dies wäre ein Vielfaches von der vorherigen Varianz von 16.

Wohingegen die Varianz wenig aussagekräftig ist, hat sie den Vorteil, dass aus ihr die aussagekräftigere Standardabweichung berechnet werden kann.

Stichprobenvarianz

Bei dem vorangegangenen Beispiel sind wir von einer Vollerhebung ausgegangen. Dies bedeutet, dass wir alle Kinder der Familie erfasst haben. Handelt es sich jedoch nur um eine Stichprobe, wird nicht durch die Anzahl der Erfassten (hier: 5 Kinder), sondern durch die Stichprobenzahl minus 1 geteilt! Die Stichprobenvarianz wird mit s² abgekürzt und wäre dann im obigen Beispiel: \[ s^2 = \frac{((1-6)^2+(3-6)^2+(5-6)^2+(9-6)^2+(12-6)^2)}{5-1} \] \[ s^2 = \frac{(80)}{4} =20 \]

2.3 Standard deviation

Die Standardabweichung ist die Quadratwurzel aus der Varianz

Berechnung:

\[ Standardabweichung = \frac{(\sqrt{(1-6)^2}+\sqrt{(3-6)^2}+\sqrt{(5-6)^2}+\sqrt{(9-6)^2}+\sqrt{(12-6)^2})}{\sqrt{5}} \] \[ Standardabweichung = \frac{\sqrt{80}}{\sqrt{5}} =4 \]

Empirische Standardabweichung

Wie auch im Beispiel zur Varianz, sind wir zunächst einmal von einer Vollerhebung ausgegangen. Handelt es sich hingegen um eine Stichprobe, wird wieder durch die Anzahl der Erfassten minus 1 geteilt:

\[ \sqrt{s^2} = \frac{(\sqrt{(1-6)^2}+\sqrt{(3-6)^2}+\sqrt{(5-6)^2}+\sqrt{(9-6)^2}+\sqrt{(12-6)^2})}{\sqrt{(5-1)}} \] \[ \sqrt{s^2} =\frac{\sqrt{80}}{\sqrt{4}} =4,47 \]

Standardabweichungen vergleichen

Nehmen wir an, in einer anderen Studie würde man das Alter nicht in Jahren, sondern in Halbjahren messen, dann hätten wir bei dem Beispiel unserer Familie 2, 6, 10, 18 und 24 Halbjahre. Als Durchschnitt hätte man demzufolge 12, die Varianz wäre 64 und die Standardabweichung 8 (mit der Rechenmethode bei einer Vollerhebung). Die Standardabweichung ist im Vergleich zum ursprünglichen Beispiel doppelt so hoch, obwohl es sich um dieselbe Familie mit derselben Streuung handelt. Der Unterschied entsteht dadurch, dass unterschiedlich gemessen wurde. Um Standardabweichungen vernünftig miteinander vergleichen zu können, müssen sie gleich gemessen werden. Eine Lösung hierfür könnte die Verwendung des Variationskoeffizienten sein, da dieser bei unserem Beispiel unabhängig von der Messung identisch wäre.

2.4 Variation coefficient

Der Variationskoeffizient ist der Quotient aus Standardabweichung und dem arithmetischen Mittelwert. Er wird üblicherweise in Prozent angegeben und ist von den zugrundeliegenden Maßeinheiten (z.B. Währungen) unabhängig. Dies ermöglicht Daten, welche in unterschiedlichen Einheiten gemessen wurden, miteinander vergleichen zu können.

Berechnung:

Zur Berechnung des Variationskoeffizienten nehmen wir die Beispieldaten unserer Familie mit den fünf Kindern her. Dabei hatten wir einen arithmetischen Mittelwert von 6 Jahren, die Varianz war 16 Jahre und die Standardabweichung betrug 4 Jahre (Vollerhebung). Die Formel des Variationskoeffizienten lautet:

\[ Variationskoeffizient = \frac{Standardabweichung}{Mittelwet} \] \[ Variationskoeffizient =\frac{4}{6} =0,67 = 66,7\% \]

Der Variationskoeffizient von 66,7% zeigt an, dass die Streuung bezogen auf den Mittelwert relativ groß ist.

Ist der arithmetische Mittelwert 0, so kann der Variationskoeffizient nicht berechnet werden (keine Teilung durch 0).

2.5 Range

Die Spannweite gilt in der Statistik als einfachstes Streuungsmaß und ist die Differenz zwischen der kleinsten und der größten Merkmalsausprägung (Differenz zwischen Min und Max einer Variablen).

Berechnung:

Bei der Familie mit fünf Kinder im Alter von 1, 3, 5, 9 und 12 Jahren, ist das Minimum 1 Jahr und das Maximum 12 Jahre. Die Spannweite errechnet sich wie folgt:

\[ Spannweite = Maximum - Minimum \] \[ Spannweite = 12 - 1 = 11 \]

Die Spannweite bei unserem Beispiel beträgt 11 Jahre. Der Median liegt bei 5 Jahren. Dieser wäre auch 5 Jahre gewesen, wenn das älteste Kind statt 12 Jahren 20 Jahre alt gewesen wäre. Die Spannweite wäre dann jedoch mit 19 (20-1) viel größer gewesen. Die Angabe eines Lageparameters (z.B. der Mittelwert oder der Median) ist daher in Kombination mit einem Streuungsparameter viel aussagekräftiger als ohne. Allerdings kann die Angabe der Spannweite auch irreführend sein.

Nehmen wir an, dass ein kompletter Monat nur um die 10 Grad Celsius hatte und nur am letzten Tag einen Höchstwert von 30 Grad Celsius erreicht hat. Demzufolge wäre die Spannweite 20 Grad Celsius (30-10) obwohl es jedoch sich eher um einen sehr kalten Monat gehandelt hat. Die Spannweite betrachtet eben nur zwei Werte aus allen Werten und diese könnten extreme Ausreißer sein.

2.6 Interquartile range

Der Interquartielsabstand (kurz IQR) ist ein Streuungsmaß in der deskriptiven Statistik. Sortiert man die Stichprobe der Größe nach, so ist der IQR der Abstand zwischen dem 3. und dem 1. Quartil. Dieser Abstand umfasst im Ergebnis die mittleren 50% der Daten.

Berechnung:

Als Beispielrechnung nehmen wir eine Familie her, welche 10 Kinder im Alter von 1, 3, 5, 7, 8, 9, 11, 12, 14 und 16 Jahren hat. Zur Bestimmung des ersten und dritten Quartils bietet sich die summary Funktion an:

a <- c(1, 3, 5, 7, 8, 9, 11, 12, 14, 16)
BigFamilie <- data.frame(a)
colnames(BigFamilie) <- c("Alter_Kinder")
summary(BigFamilie$Alter_Kinder)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1.00    5.50    8.50    8.60   11.75   16.00

Die Formel für den IQR lautet:

\[ IQR = 3.Quartil - 1.Quartil \] \[ IQR = 11,75-5,50 = 6,25 \]

In einem Boxplot ist der Interquartilsabstand durch die Kantenlänge der “Box” gekennzeichnet.

boxplot(BigFamilie, ylab = "age", main = "Boxplot for IQR demonstration")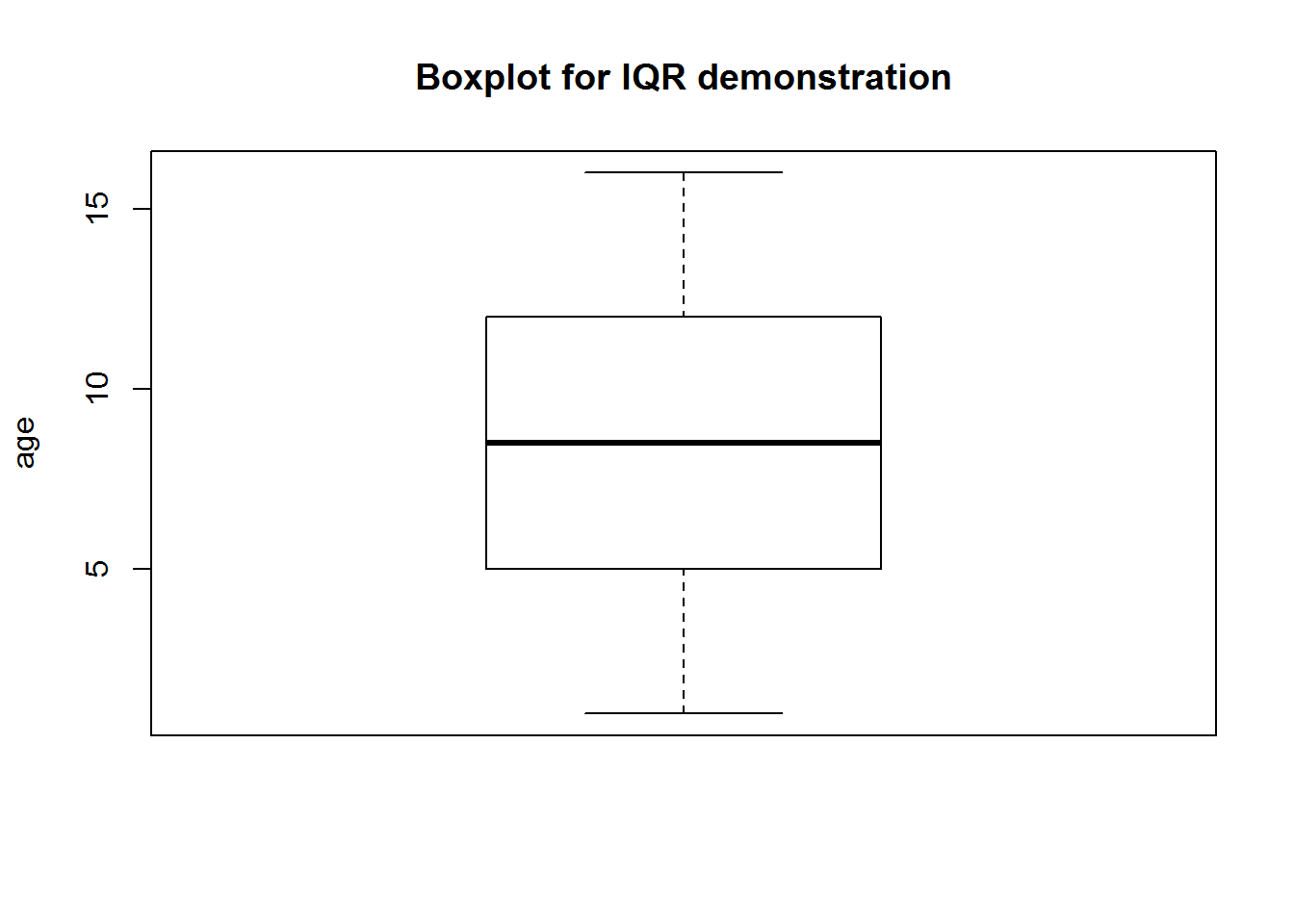

Dadurch dass die oberen und unteren 25% der Daten nicht einbezogen werden, ist der IQR als Streuungsmaß robust gegenüber Ausreißern.