Table of Content
- 1 Introduction
- 2 Overview
- 3 Type of Graphs
- 3.1 Bar Graph
- 3.2 Histogram
- 3.3 Scatter Plot
- 3.4 Line Graph
- 3.5 Box Plot
- 4 Labeling and further commands
- 5 Conclusion
1 Introduction
In dem nachfolgenden Post geht es um eine kurze Einführung zum Thema Visualisierung. Es sollen die am häufigsten verwendeten Grafiken in R vorgestellt werden und wann sie zu verwenden sind. Für diese Arbeit wurde der Datensatz insurance von der Statsistik-Plattform Kaggle https://www.kaggle.com verwendet. Eine Kopie des Datensatzes ist unter https://drive.google.com/file/d/1-DSBcvyFtXrSy1ORb6WOeNenhQ1rxSYu/view?usp=drivesdk abrufbar.
library("tidyverse")
library("mosaic")insurance <- read_csv("insurance.csv")2 Overview
glimpse(insurance)## Observations: 1,338
## Variables: 7
## $ age <int> 19, 18, 28, 33, 32, 31, 46, 37, 37, 60, 25, 62, 23, 5...
## $ sex <chr> "female", "male", "male", "male", "male", "female", "...
## $ bmi <dbl> 27.900, 33.770, 33.000, 22.705, 28.880, 25.740, 33.44...
## $ children <int> 0, 1, 3, 0, 0, 0, 1, 3, 2, 0, 0, 0, 0, 0, 0, 1, 1, 0,...
## $ smoker <chr> "yes", "no", "no", "no", "no", "no", "no", "no", "no"...
## $ region <chr> "southwest", "southeast", "southeast", "northwest", "...
## $ charges <dbl> 16884.924, 1725.552, 4449.462, 21984.471, 3866.855, 3...Der Datensatz insurance beinhaltet 7 Variablen. Bis auf die Spalten bmi und children kommen alle Variablen in der weiteren Analyse zur Anwendung.
3 Type of Graphs
Grafiken sind ein wichtiger Bestandteil bei der deskriptiven Untersuchung von Datensätzen. Durch sie können komplizierte und uneinsichtige Sachverhalt einfach beschrieben und dargestellt werden. Jedem sollte jedoch klar sein, dass es sich bei Publikationen oder Bachelorarbeiten um eine wissenschaftliche Arbeit handelt und nicht um ein Bilderbuch. Deshalb empfiehlt es sich, eine Bilderflut möglichst zu vermeiden und nur wirklich aussagekräftige Grafiken zu verwenden.
3.1 Bar Graph
Ein Balkendiagramm eignet sich zur grafischen Darstellung der Häufigkeit von Ausprägungen beliebig skalierter Merkmale. Dabei können sowohl absolute als auch relative Häufigkeiten darstellen werden. Mit dem nachfolgenden Balkendiagramm soll schnell und einfach herausgefunden werden, wie die uns vorliegende Geschlechterverteilung aussieht.
qplot(insurance$sex, geom = "bar")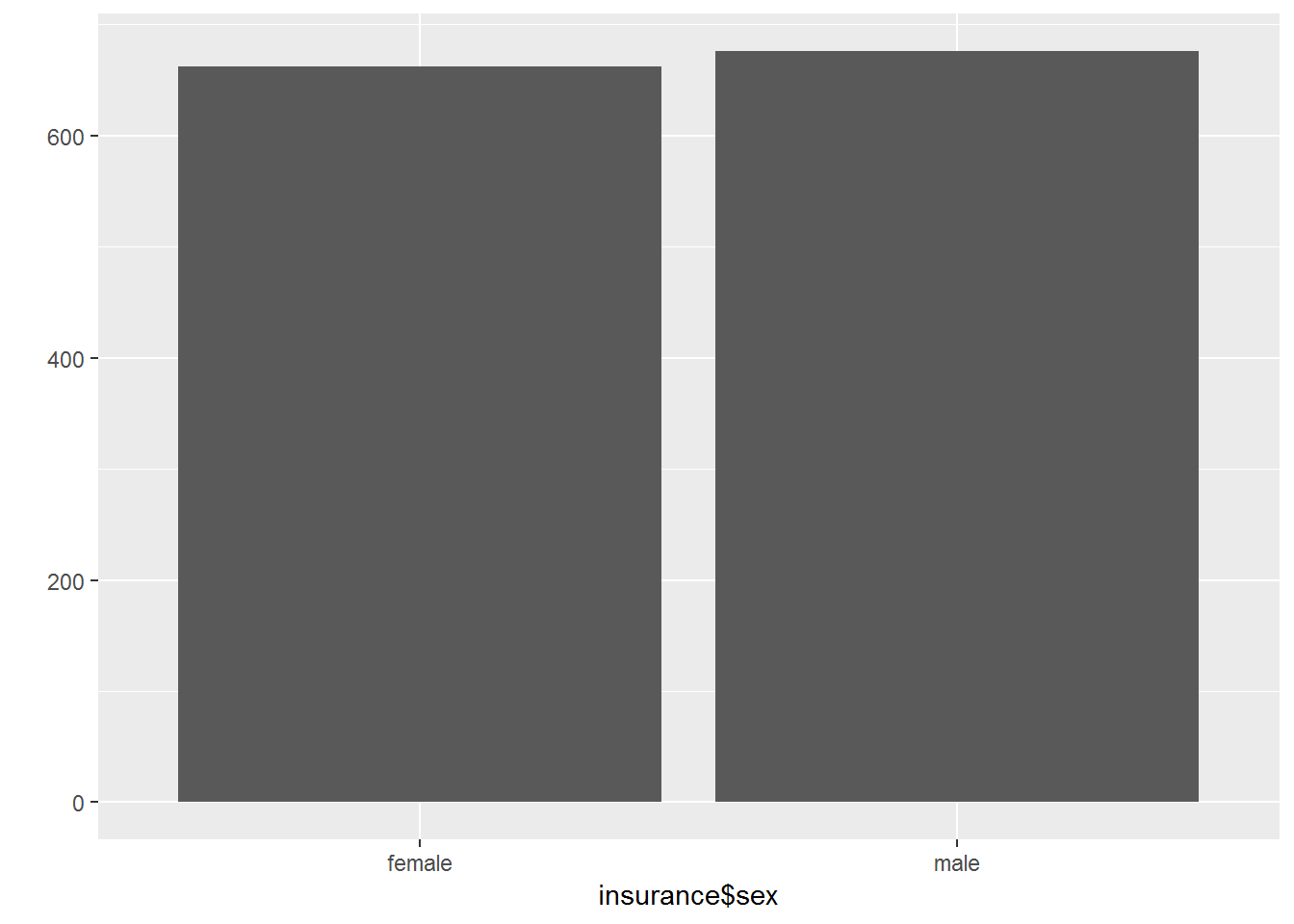
Balkendiagramme kann man ab nominalem Skalenniveau für eine anschauliche Darstellung einsetzen. Bei metrischen Datenmaterial ist allerdings für zusätzliche Informationen das Histogramm vorzuziehen. Denn bei diesem stellt der Flächeninhalt einer Säule die Häufigkeit und ihre Höhe die Häufigkeitsdichte dar.
3.2 Histogram
Zur graphischen Darstellung klassierter Daten verwendet man das Histogramm. Ein Histogramm ist nun analog zu einem Balkendiagramm zu sehen, mit dem wesentlichen Unterschied, dass die Flächen der Säulen hier die (absoluten oder relativen) Häufigkeiten widergeben und nicht ihre Höhen.
hist(insurance$age)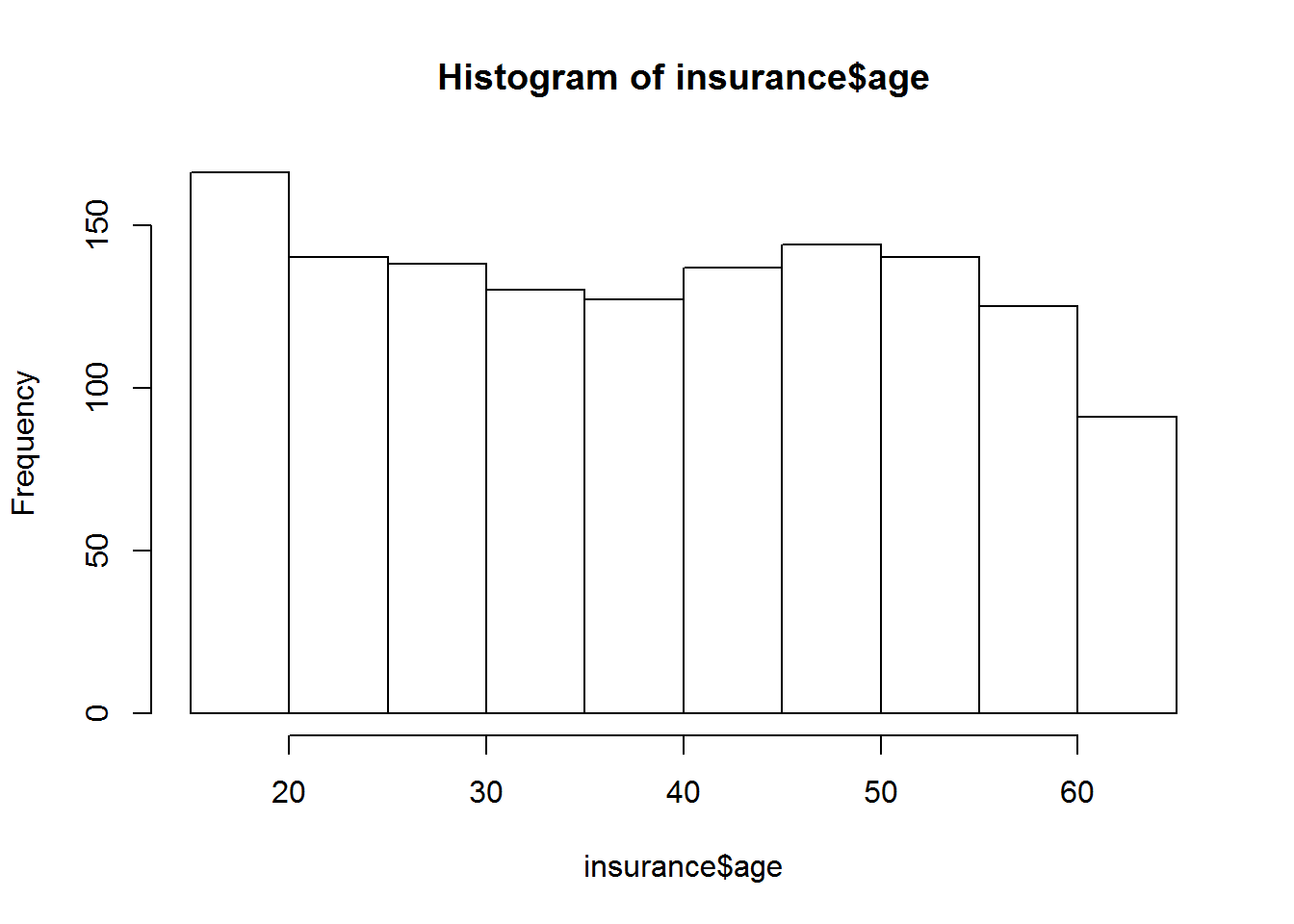
Den Unterschied zum Balkendiagramm kann man sehr gut erkennen, wenn man mit dem Befehlt breaks arbeitet. Mit breaks kann man bestimmen, wie viele Balken in der Grafik ausgegeben werden sollen. Kreiert man mehr Balken als es Klassifizierungen gibt, so kann man deren Höhe wiederum an der y Achse ablesen.
summary(insurance$age)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 18.00 27.00 39.00 39.21 51.00 64.00par(mfrow=c(1,2))
hist(insurance$age, breaks=64)
hist(insurance$age, breaks=80)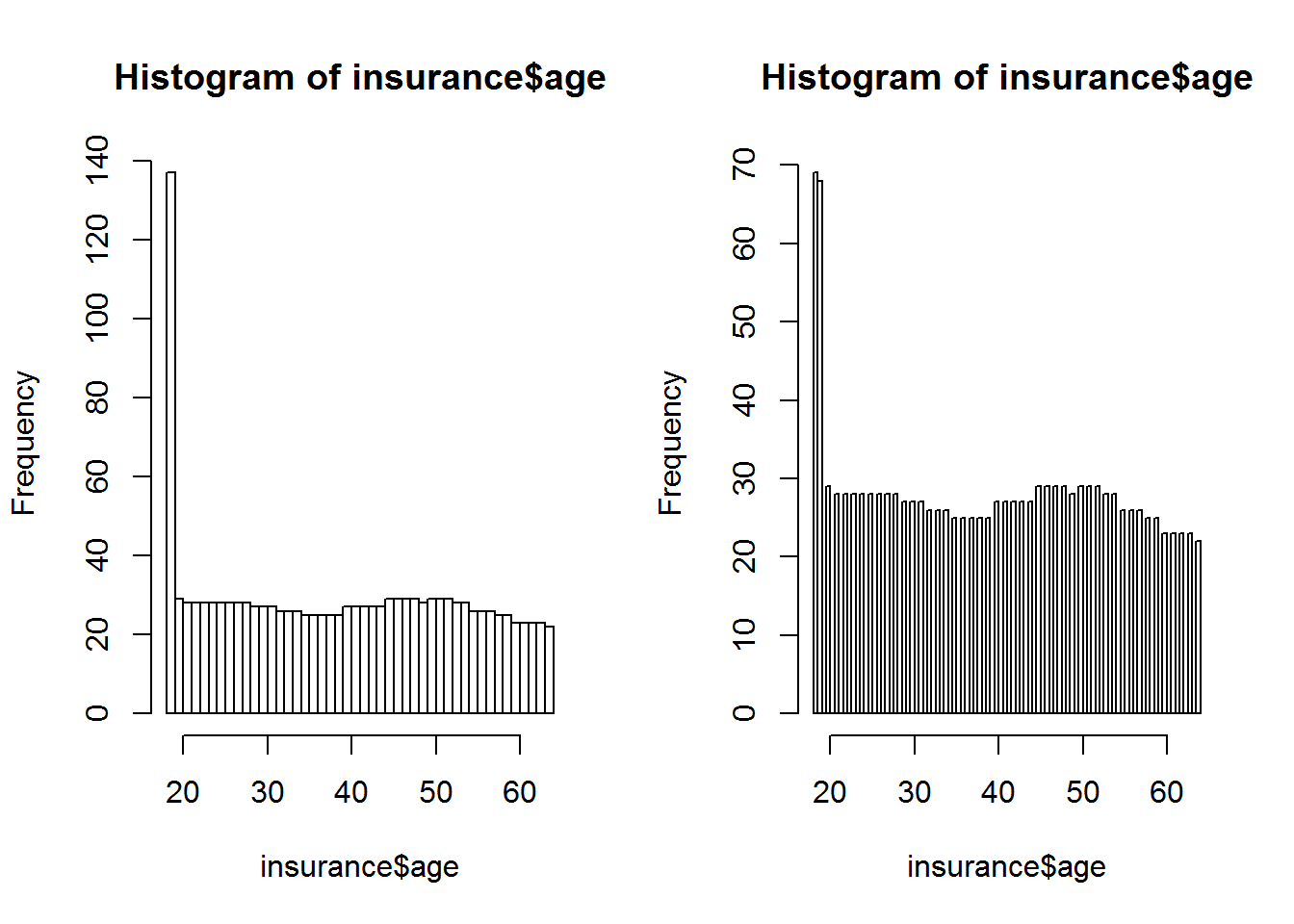
In der linken Grafik werden die unter 20 jährigen noch in einem Balken zusammengefasst. Daher erhöht sich ihre Gesamtsumme auf knapp 140. Im rechten Bild sind diese bereits getrennt und man erkennt zwei Ausprägungen nahe n = 70. Mit dem tally() Befehlt aus dem mosaic Package, kann man sich die Häufigkeiten auch einfach und schnell ausgeben lassen:
tally (~insurance$age)## insurance$age
## 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
## 69 68 29 28 28 28 28 28 28 28 28 27 27 27 26 26 26 25 25 25 25 25 27 27 27
## 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
## 27 27 29 29 29 29 28 29 29 29 28 28 26 26 26 25 25 23 23 23 23 22Die obere Zeile gibt das jeweilige Alter aus und die darunter liegende Zeile die entsprechende Häufigkeit. Wir können hier sehen, dass 69 Probanden 18 Jahre alt und 68 Probanden 19 Jahre alt sind. Die restlichen Altersklassen sind alle etwa gleich stark vertreten.
3.3 Scatter Plot
In einem Streudiagramm werden in einem Koordinatensystem die Werte zweier metrischer Merkmale abgetragen, um etwaige Zusammenhänge bzw. Korrelationen erkennen zu können. Üblicherweise wird die unabhängige bzw. erklärende Variable auf der horizontalen x-Achse und die abhängige Variable auf der vertikalen y-Achse abgetragen.
par(mfrow=c(1,1))
plot(insurance$age, insurance$charges)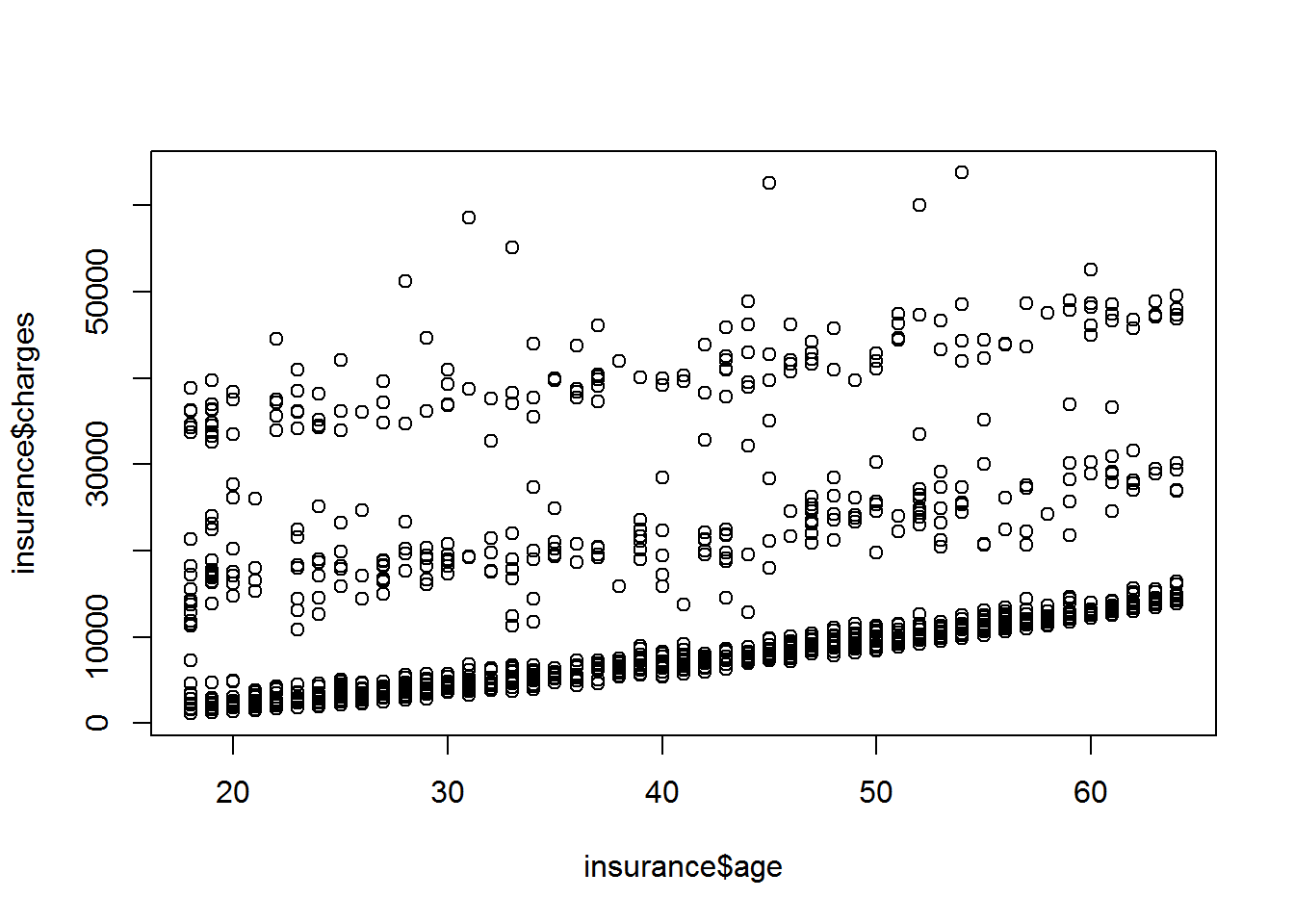
Es scheint einen leichten Zusammenhang zwischen dem Lebensalter und der Höhe der Versicherungskosten zu geben. Des Weiteren fällt auf, dass zwei weitere Gruppen vermutlich existieren, welche weitaus höheren Kosten verursachen.
3.4 Line Graph
Das Liniendiagramm eignet sich hauptsächlich zur Visualisierung von Trends und Entwicklungen im Laufe der Zeit bei gleichmäßig unterteilten Dimensionswerten wie Monaten, Quartalen oder Jahren. Ein Datensatz muss mindestens zwei Datenpunkte enthalten, um eine Linie zu zeichnen. Ein Datensatz mit nur einem einzigen Wert wird als Punkt dargestellt. Im Gegensatz zum Streudiagramm kann es jeweils nur ein Wertepaar bzw. Wertetrio geben. Da der uns vorliegende Datensatz insurance keine geeignete Variablen für diese Grafik bieten kann, wird mittels R ein neuer data.frame erzeugt.
x <- c(2, 5, 7, 9, 13, 14, 17, 19, 22, 25, 28, 30)
y <- c(11, 13, 17, 23, 33, 35, 55, 65, 70, 75, 80, 85)
example1 <- data.frame(x, y)
colnames(example1) <- c("age", "weight")
example1## age weight
## 1 2 11
## 2 5 13
## 3 7 17
## 4 9 23
## 5 13 33
## 6 14 35
## 7 17 55
## 8 19 65
## 9 22 70
## 10 25 75
## 11 28 80
## 12 30 85Nun kann graphisch dargestellt werden, wie das Körpergewicht über die Lebensjahre hinweg bei einer Person zunimmt.
par(mfrow=c(1,2))
plot(example1$age, example1$weight, type = "l")
plot(example1$age, example1$weight, type = "l") +
points(example1$age, example1$weight)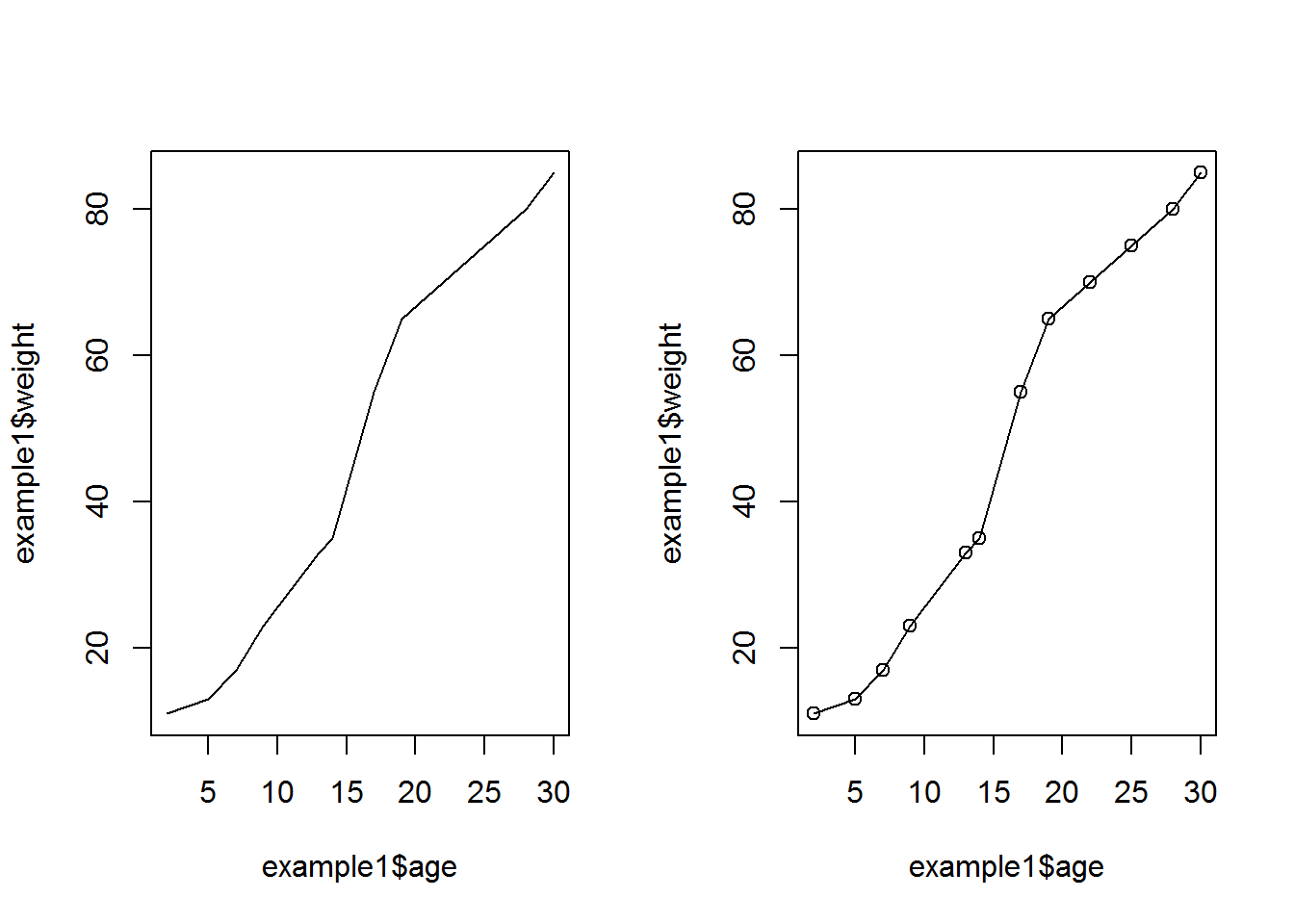
## integer(0)Dies ist nur ein exemplarisches Beispiel, welches zur Veranschaulichung dienen soll. Möchte man sich die einzelnen Punkte, welche dem Liniendiagramm zu Grunde liegen, zusätzlich ausgeben lassen, so muss die plot Funktion um den Befehlt points() erweitert werden.
3.5 Box Plot
Ein Boxplot ist eine grafische Zusammenfassung der folgenden fünf Punkte:
- Minimum (= 0%-Quantil)
- 25%-Quantil
- Median (= 50%-Quantil)
- 75%-Quantil
- Maximum (= 100%-Quantil)
Da man das Minimum, den Median und das Maximum als 0%-, 50%- bzw. 100%-Quantil ausdrücken kann, zeigt der Boxplot nur fünf häufig verwendete Quantile. Dabei ist die Box und ihre sogenannten “Whiskers”, die Striche außerhalb der Boxen, wie folgt aufgebaut: Die Box spannt sich vom 25%-Quantil bis zum 75%-Quantil auf, in ihr ist der Median durch einen Querstrich markiert. Außerhalb der Boxen spannen sich nach oben und unten die Whiskers zum Minimum bzw. Maximum der Datenreihe. Am Boxplot kann man auch zwei Streuungsmaße ablesen: Die Spannweite ist nämlich der Abstand zwischen den beiden Whiskers (bzw. zwischen den äußersten Ausreißern). Der Interquartilsabstand ist genau die Breite der Box.
par(mfrow=c(1,1))
boxplot(insurance$charges)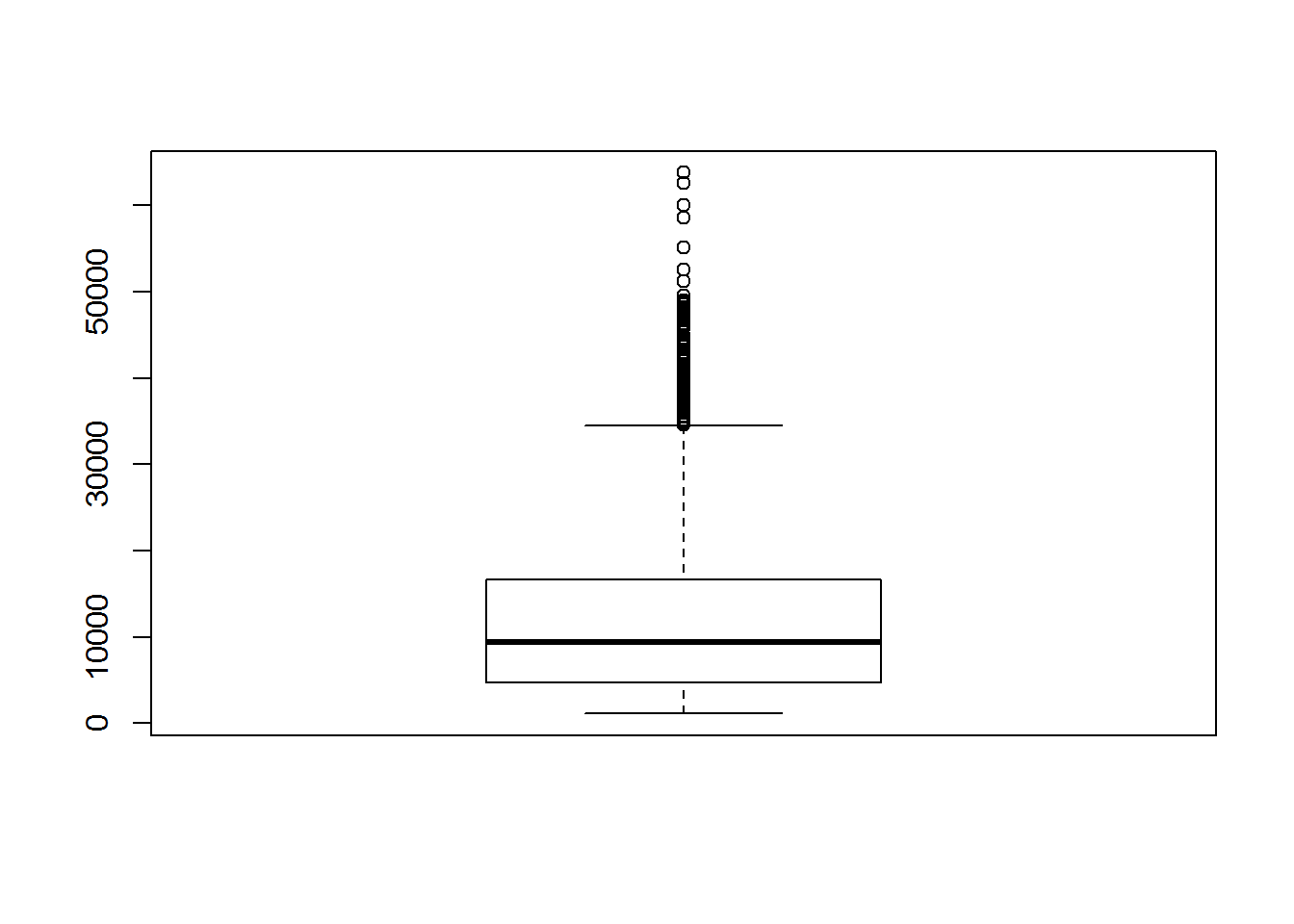
Das Boxplot zu den Versicherungskosten zeigt uns, dass die meisten Gebühren zwischen 5.000$ und 20.000$ liegen. Ebenfalls sind die Ausreißer jenseits der 50.000 Marke gut ersichtlich.
Man kann sich auch die Verteilung der Versicherungskosten pro Geschlecht…
plot(as.factor(insurance$sex), insurance$charges)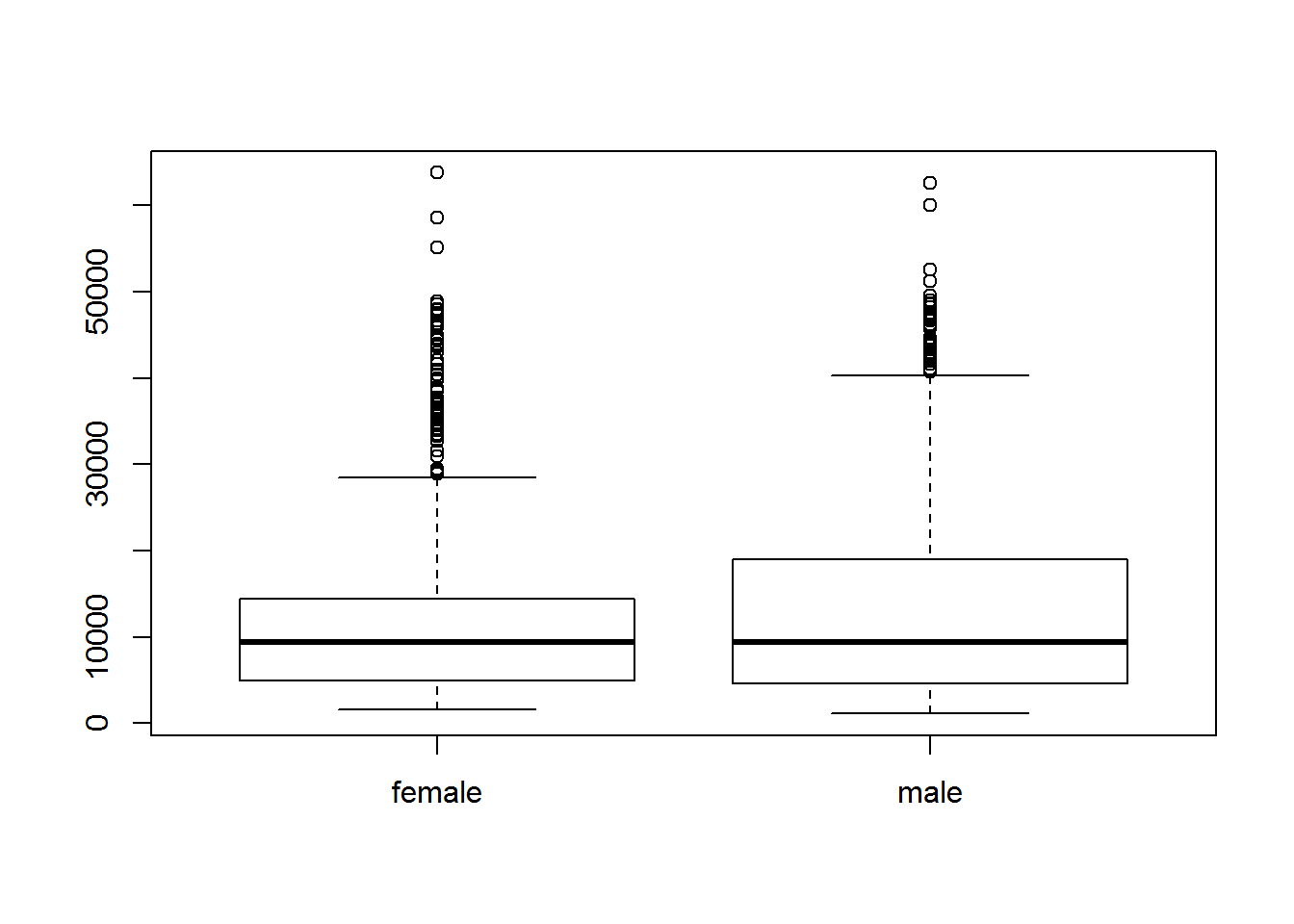
und pro Region ausgeben lassen.
plot(as.factor(insurance$region), insurance$charges)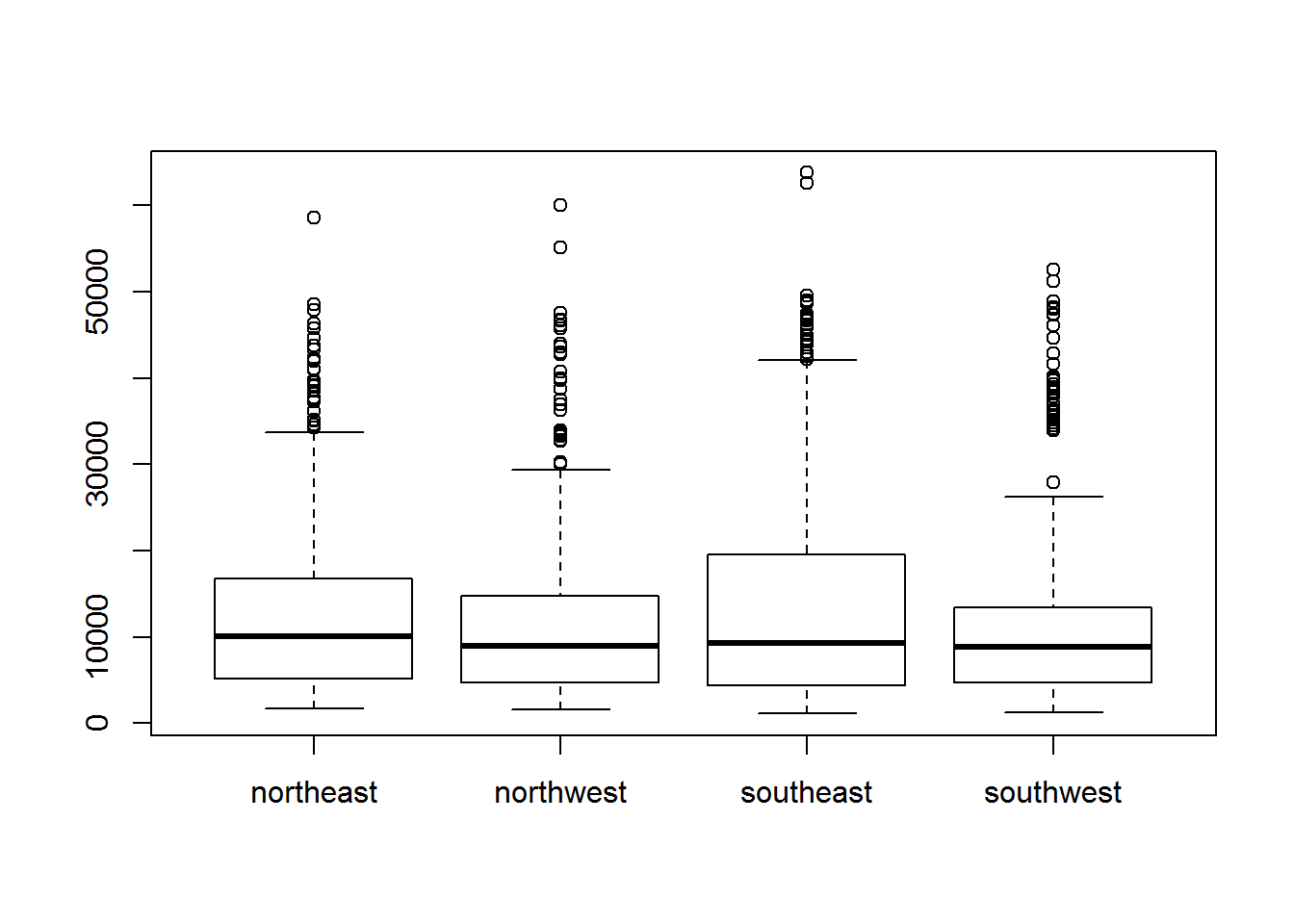
4 Labeling and further commands
Die von R ausgegebenen Beschriftungen sind meist sehr unschön oder fehlen gänzlich. Daher hier noch ein paar Tipps anhand des zuvor erstellten Scatter Plot Beispiels, damit die erstellten Grafiken ein wenig hübscher und aussagekräftiger werden.
plot(insurance$age, insurance$charges)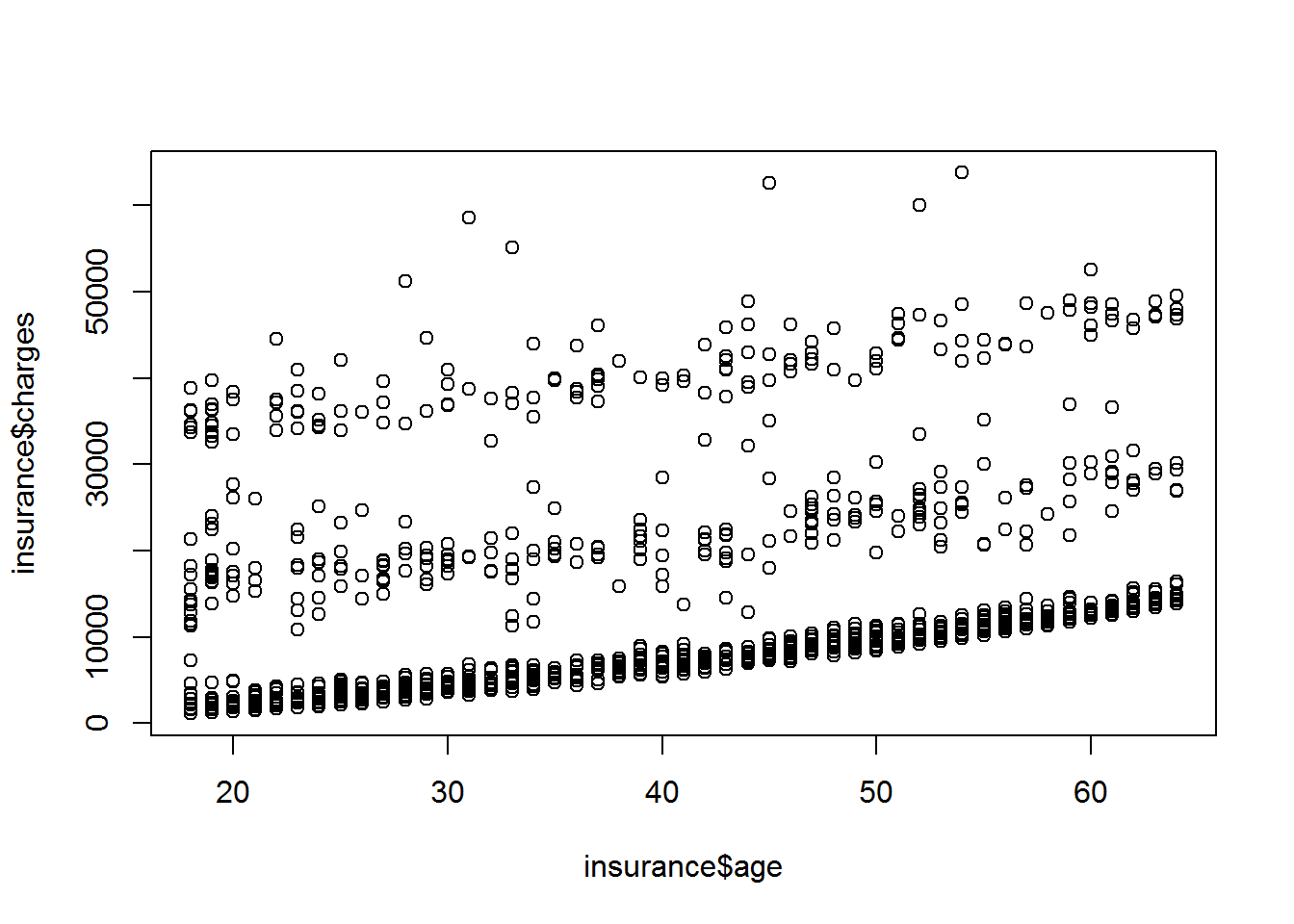
Die Befehle xlab und ylab ermöglichen eine Beschriftung der beiden Achsen. Mit main kann eine Überschrift hinzugefügt werden.
plot(insurance$age, insurance$charges, xlab = "age", ylab = "charges", main = "Scatter Plot", pch=19)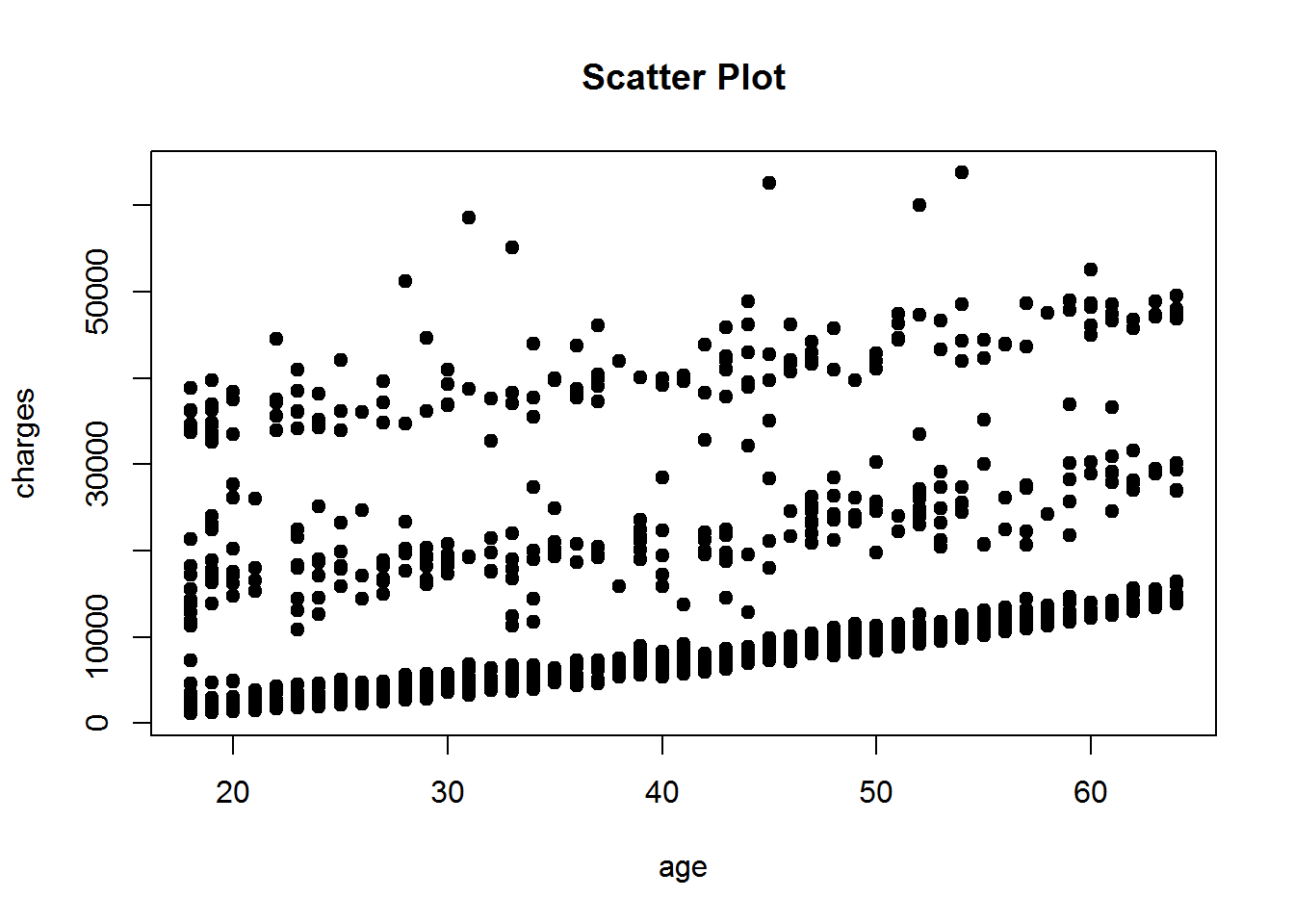
Der Zusatzbefehl pch ist von 0 bis 25 möglich. Für jede Zahl werden unterschiedliche Arten von Punkten generiert.
plot(insurance$age, insurance$charges, xlab = "age", ylab = "charges", main = "Scatter Plot", pch=19, col=factor(insurance$smoker))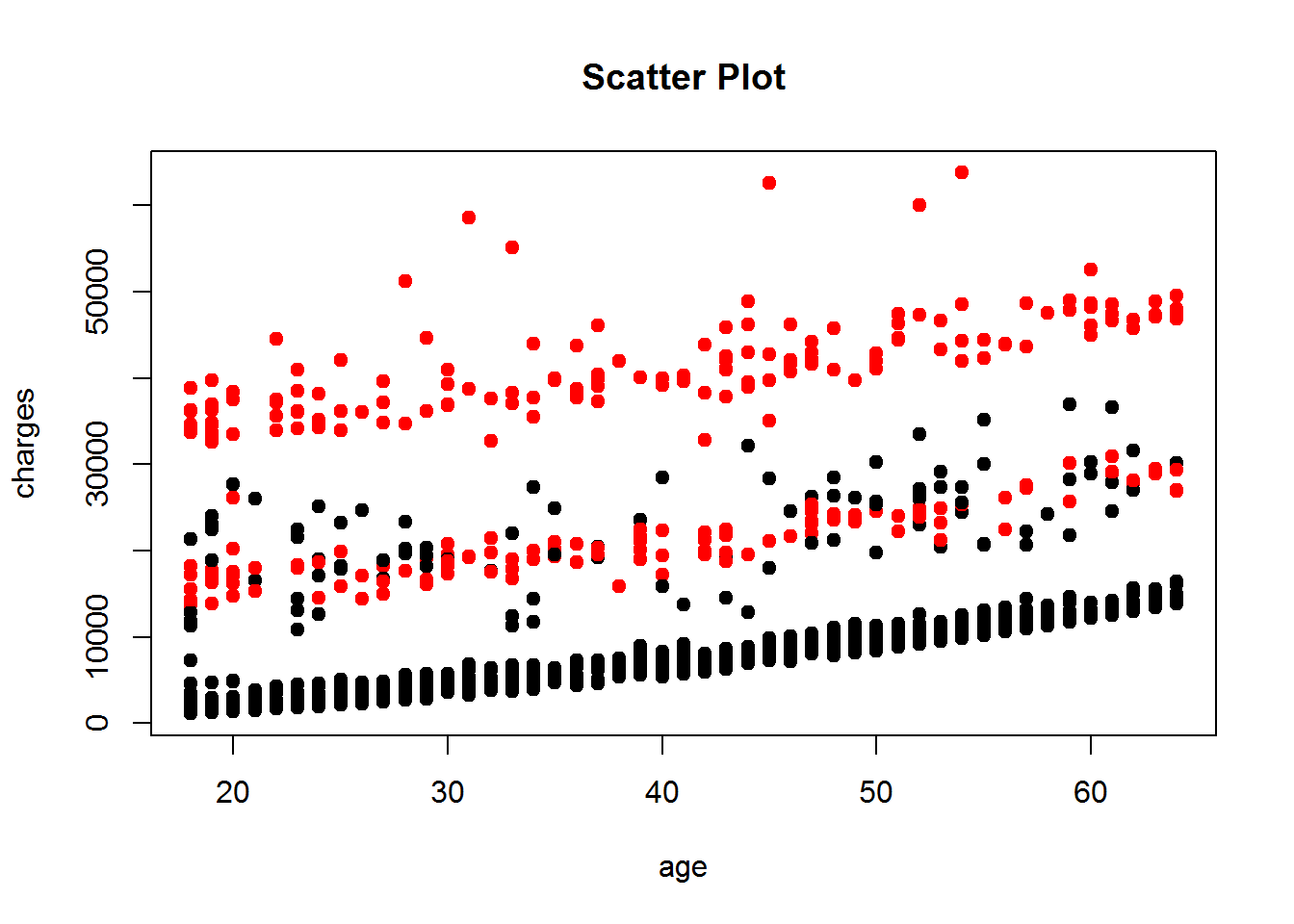
Wie schon bei Punkt 3.3 Scatter Plot vermutet, exisiteren bei Zusammenhang zwischen Lebensalter und Versicherungskosten weitere Gruppierungen. Durch den Befehl col wurden die Raucher unter den Probanden farblich hervorgehoben. Man erkennt eindeutig, dass Raucher höhere Versicherungskosten verursachen als Nichtraucher. Diese sind ab der 40.000 Marke gar nicht mehr in der Grafik vertreten. Des Weiteren könnte man nun vermuten, dass das mittlere Segment zwischen 10.000$ und 30.000$ nur leichte Raucher beinhaltet und ab 30.000$ Kosten starke Raucher vertreten sind.
5 Conclusion
Es braucht nicht viel um in R schnell und einfach verschiedene Arten von Grafiken zu erstellen. Grafiken helfen uns dabei einen guten Überblick über die uns vorliegenden Daten zu bekommen. In diesem Post wurde lediglich auf die einfachste Verwendung der Grafiken eingegangen. Bei der Visualizierung ist noch viel mehr möglich und teilweise auch nötig, um aussagekräftige Schaubilder zu generieren.