Introduction

In der nachfolgenden Fallstudie geht es um die exemplarische Analyse nominaler Daten anhand des Untergangs der Titanic. Es soll der Hauptfrage nachgegangen werden, ob das Reisen in einer besseren Klasse die Überlebenschancen auf der Titanic erhöht hat. Für diese Untersuchung wurde der Datensatz titanic_train von der Statsistik-Plattform Kaggle https://www.kaggle.com verwendet. Eine Kopie des Datensatzes ist unter https://drive.google.com/file/d/1Q-ISaCWBl9q2egJgzgkOmWndDeBa5EXT/view?usp=drivesdk abrufbar.

library("tidyverse")
library("compute.es")

Titanic <- read_csv("Titanic.csv")

Overview

Ein erster Blick auf die Daten zeigt uns, welche Variablen mit wie vielen Observations vorliegen.

glimpse(Titanic)

## Observations: 891
## Variables: 12
## $ PassengerId <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,...
## $ Survived    <int> 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0,...
## $ Pclass      <int> 3, 1, 3, 1, 3, 3, 1, 3, 3, 2, 3, 1, 3, 3, 3, 2, 3,...
## $ Name        <chr> "Braund, Mr. Owen Harris", "Cumings, Mrs. John Bra...
## $ Sex         <chr> "male", "female", "female", "female", "male", "mal...
## $ Age         <dbl> 22, 38, 26, 35, 35, NA, 54, 2, 27, 14, 4, 58, 20, ...
## $ SibSp       <int> 1, 1, 0, 1, 0, 0, 0, 3, 0, 1, 1, 0, 0, 1, 0, 0, 4,...
## $ Parch       <int> 0, 0, 0, 0, 0, 0, 0, 1, 2, 0, 1, 0, 0, 5, 0, 0, 1,...
## $ Ticket      <chr> "A/5 21171", "PC 17599", "STON/O2. 3101282", "1138...
## $ Fare        <dbl> 7.2500, 71.2833, 7.9250, 53.1000, 8.0500, 8.4583, ...
## $ Cabin       <chr> NA, "C85", NA, "C123", NA, NA, "E46", NA, NA, NA, ...
## $ Embarked    <chr> "S", "C", "S", "S", "S", "Q", "S", "S", "S", "C", ...

Bestimmung der univariaten Häufigkeiten

Der zu Beginn gestellten Hauptfrage nach, sind für diese Fallstudie nur zwei von den zwölf uns vorliegenden Variablen interessant: Survived und Pclass. Obwohl beide Variablen im Datensatz mit Zahlen hinterlegt sind, handelt es sich um kategorial verteilte Daten (nicht-metrisch). Diese sollen im ersten Schritt ausgezählt werden. Für die nachfolgende Analyse interessiert uns, wie viele Passagiere es pro Klasse gab und wie viele aus der jeweiligen Klasse die Katastrophe überlebten.

Frequency_Class <- count(Titanic, Survived) 
Frequency_Class

## # A tibble: 2 x 2
##   Survived     n
##      <int> <int>
## 1        0   549
## 2        1   342

Jetzt ist klar, dass 549 Menschen den Untergang der Titanic nicht überlebt haben. Dies in einem Balkendiagramm dargestellt:

ggplot(Titanic, aes(x = Survived)) +
  geom_bar() +
  ggtitle("Frequency Survived") + 
  xlab("Survived, 0 = No / 1 = Yes") + 
  ylab("Count")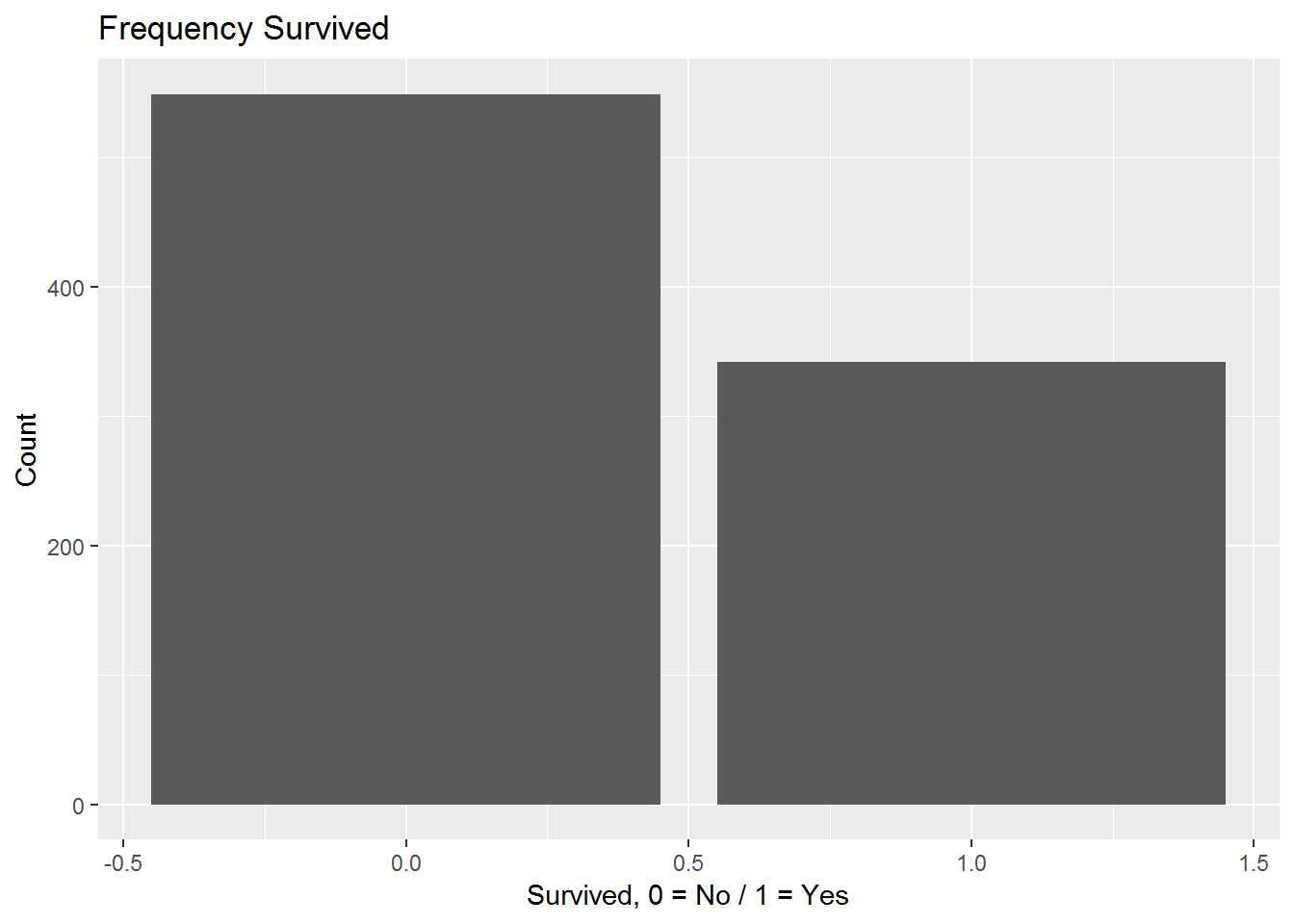

Und wie sieht es mit der Verteilung auf die verschiedenen Klassen aus?

Frequency_Class <- count(Titanic, Pclass) 
Frequency_Class

## # A tibble: 3 x 2
##   Pclass     n
##    <int> <int>
## 1      1   216
## 2      2   184
## 3      3   491

ggplot(Frequency_Class, aes(x = factor(Pclass), y = n)) +
  geom_point(size = 3, colour = "red") +
  ggtitle("Frequency Class") + 
  xlab("Class") + 
  ylab("Count")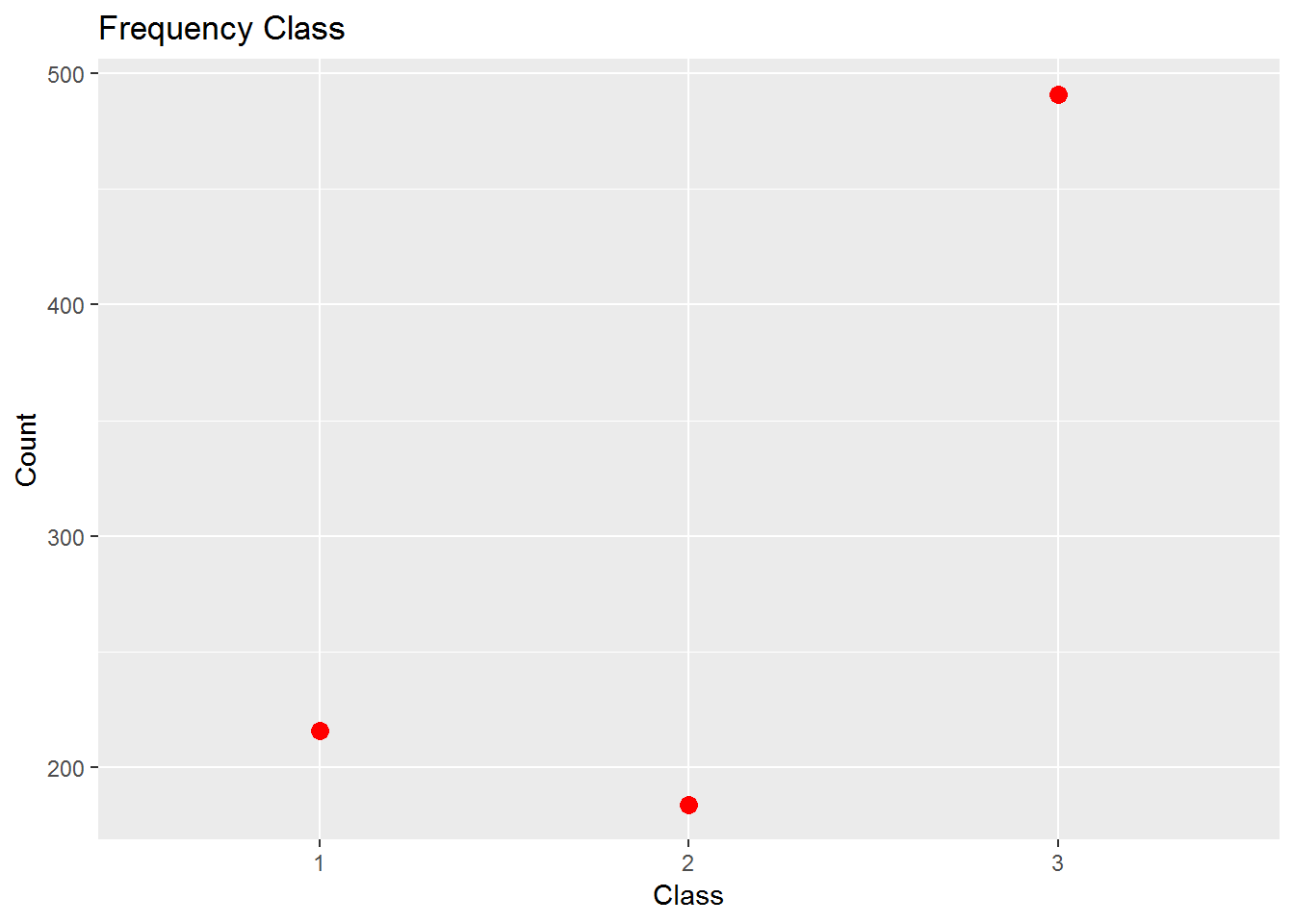

Doch 1/4 der Passagiere reisten damals in der ersten Klasse.

Bestimmung der bivariaten Häufigkeiten

Nachdem nun die Häufigkeiten pro Wert von Survived und Pclass bekannt sind, wird nun der Frage nachgegangen, ob sich die relativen Häufigkeiten der Stufen der Klasse innerhalb der Stufen der Überlebenden unterscheidet. Es soll untersucht werden, ob und in wie weit die Überlebenschancen in der 1. Klasse größer als in der 2. oder 3. Klasse sind.

(Frequency_Survived_Class <- count(Titanic, Survived, Pclass))

## # A tibble: 6 x 3
##   Survived Pclass     n
##      <int>  <int> <int>
## 1        0      1    80
## 2        0      2    97
## 3        0      3   372
## 4        1      1   136
## 5        1      2    87
## 6        1      3   119

ggplot(Frequency_Survived_Class, aes(x = factor(Pclass), y = n, color = factor(Survived))) +
  geom_point(size = 3) +
  ggtitle("Frequency Survived & Class") + 
  xlab("Class") + 
  ylab("Count") + 
  guides(color=guide_legend(title = "Survived?\n0 = No / 1 = Yes"))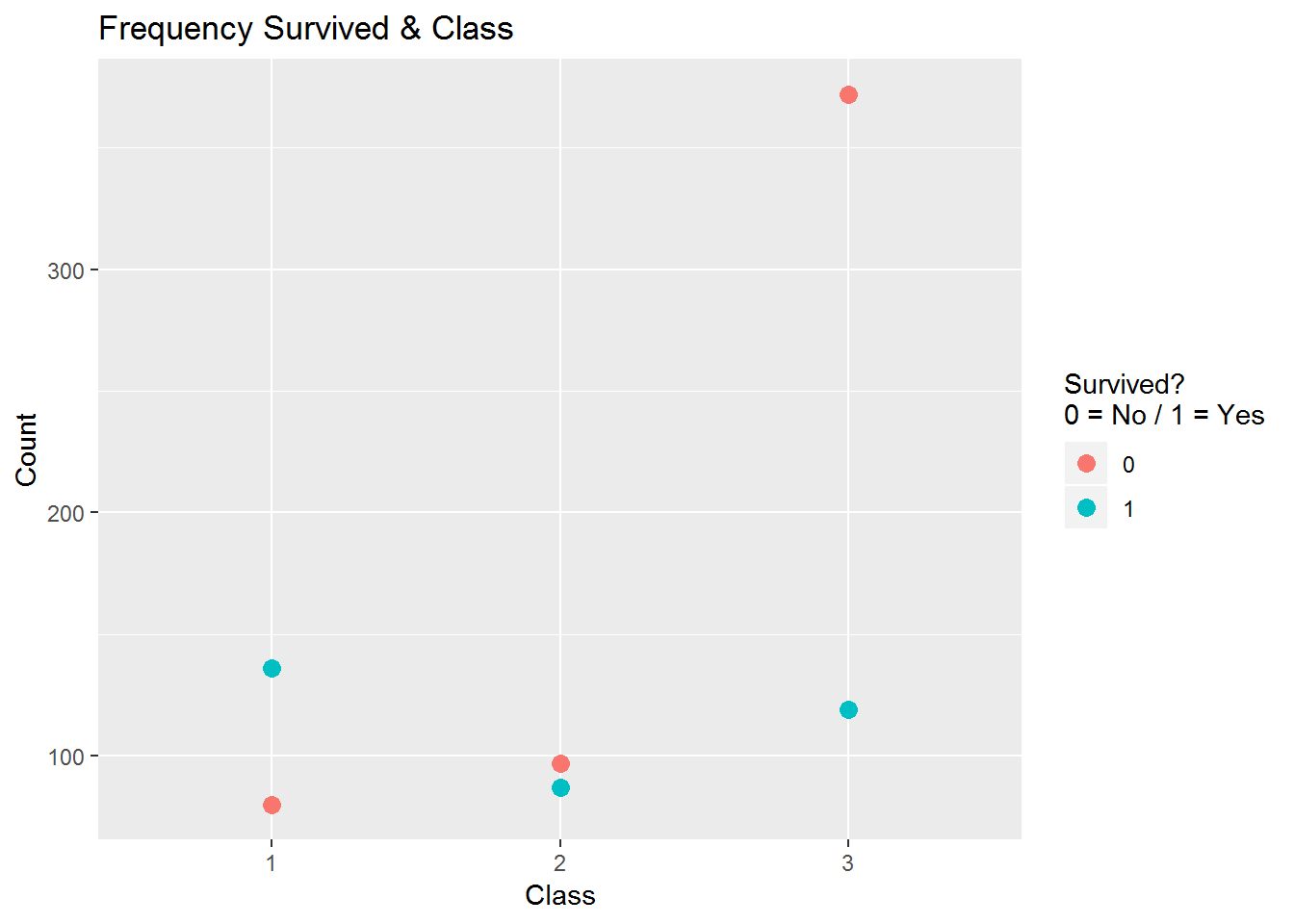

Signifikanztest

Für die Untersuchung, ob es einen Unterschied zu den Überlebenschancen zwischen den verschiedenen Klassen gibt, werden die Variablen Survived und Pclass einem Signifikanztest unterzogen. An dieser Stelle soll erwähnt sein, dass ein p-Wert eine Funktion der Stichprobengröße ist. Er gibt nicht die Wahrscheinlichkeit der getesteten Hypothese an. Ein p-Wert gibt lediglich an, wie wahrscheinlich der beobachtete Prüfgrößenwert oder ein in Richtung der Alternative noch extremerer Wert unter der Nullhypothese ist. Für die nachfolgende Untersuchung auf Signifikanz bietet sich in diesem Fall der Chi-Quadrat-Test an.

chisq.test(Titanic$Survived, Titanic$Pclass)

## 
##  Pearson's Chi-squared test
## 
## data:  Titanic$Survived and Titanic$Pclass
## X-squared = 102.89, df = 2, p-value < 2.2e-16

Da der ausgegebene p-Wert unter dem Signifikanzniveau von 5% liegt, kann weiter daran geglaubt werden, dass es einen Unterschied zwischen den Klassen hinsichtlich der Überlebenschanchen gibt.

Effektstärke

Da ein p-Wert alleine nicht besonders stark aussagekräftig ist, wird im folgenden Schritt das Chancen Verhältnis “Odds Ratio” (OR) errechnet. Das OR ist definiert für 2*2 - Häufigkeitstabellen und errechnet um welchen Faktor die Überlebenschanche in der einen Klasse größer als in der anderen Klasse ist.

Effektstärke Klasse 1 und 2

Es wird erneut ein Chi-Quadrat-Test durchgeführt, denn durch die Einschränkung auf nur zwei Klassen verändert sich der X-squared Wert des Tests.

Class1_2 <- Titanic %>% filter(Pclass == 1 | Pclass == 2)
chisq.test(Class1_2$Survived, Class1_2$Pclass)

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  Class1_2$Survived and Class1_2$Pclass
## X-squared = 9.2775, df = 1, p-value = 0.00232

Außerdem wird für die Berechnung des Chancen Verhältnisses die Anzahl der Personen der beiden Klassen benötigt:

nrow(Class1_2)

## [1] 400

chies(chi.sq = 9.2775, n = nrow(Class1_2))

## Mean Differences ES: 
##  
##  d [ 95 %CI] = 0.31 [ 0.11 , 0.51 ] 
##   var(d) = 0.01 
##   p-value(d) = 0 
##   U3(d) = 62.09 % 
##   CLES(d) = 58.61 % 
##   Cliff's Delta = 0.17 
##  
##  g [ 95 %CI] = 0.31 [ 0.11 , 0.51 ] 
##   var(g) = 0.01 
##   p-value(g) = 0 
##   U3(g) = 62.07 % 
##   CLES(g) = 58.6 % 
##  
##  Correlation ES: 
##  
##  r [ 95 %CI] = 0.15 [ 0.05 , 0.25 ] 
##   var(r) = 0 
##   p-value(r) = 0 
##  
##  z [ 95 %CI] = 0.15 [ 0.05 , 0.25 ] 
##   var(z) = 0 
##   p-value(z) = 0 
##  
##  Odds Ratio ES: 
##  
##  OR [ 95 %CI] = 1.75 [ 1.22 , 2.51 ] 
##   p-value(OR) = 0 
##  
##  Log OR [ 95 %CI] = 0.56 [ 0.2 , 0.92 ] 
##   var(lOR) = 0.03 
##   p-value(Log OR) = 0 
##  
##  Other: 
##  
##  NNT = 10.34 
##  Total N = 400

Das Odds Ratio für Klasse 1 und 2 beträgt 10,34. Das bedeutet, die Überlebenschance ist in Klasse 1 ist 10 mal höher als in Klasse 2. Diese Untersuchung soll im Nachfolgenden für die Klassen 2 & 3 und 1 & 3 ebenfalls durchgeführt werden.

Effektstärke Klasse 2 und 3

Class2_3 <- Titanic %>% filter(Pclass == 2 | Pclass == 3)
chisq.test(Class2_3$Survived, Class2_3$Pclass)

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  Class2_3$Survived and Class2_3$Pclass
## X-squared = 32.447, df = 1, p-value = 1.225e-08

nrow(Class2_3)

## [1] 675

chies(chi.sq = 32.447, n = nrow(Class2_3))

## Mean Differences ES: 
##  
##  d [ 95 %CI] = 0.45 [ 0.29 , 0.6 ] 
##   var(d) = 0.01 
##   p-value(d) = 0 
##   U3(d) = 67.33 % 
##   CLES(d) = 62.46 % 
##   Cliff's Delta = 0.25 
##  
##  g [ 95 %CI] = 0.45 [ 0.29 , 0.6 ] 
##   var(g) = 0.01 
##   p-value(g) = 0 
##   U3(g) = 67.31 % 
##   CLES(g) = 62.45 % 
##  
##  Correlation ES: 
##  
##  r [ 95 %CI] = 0.22 [ 0.15 , 0.29 ] 
##   var(r) = 0 
##   p-value(r) = 0 
##  
##  z [ 95 %CI] = 0.22 [ 0.15 , 0.3 ] 
##   var(z) = 0 
##   p-value(z) = 0 
##  
##  Odds Ratio ES: 
##  
##  OR [ 95 %CI] = 2.26 [ 1.7 , 2.99 ] 
##   p-value(OR) = 0 
##  
##  Log OR [ 95 %CI] = 0.81 [ 0.53 , 1.1 ] 
##   var(lOR) = 0.02 
##   p-value(Log OR) = 0 
##  
##  Other: 
##  
##  NNT = 6.79 
##  Total N = 675

Die Chance zu Überleben ist in Klasse 2 fast 7mal größer als in Klasse 3.

Effektstärke Klasse 1 und 3

Class1_3 <- Titanic %>% filter(Pclass == 1 | Pclass == 3)
chisq.test(Class1_3$Survived, Class1_3$Pclass)

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  Class1_3$Survived and Class1_3$Pclass
## X-squared = 95.893, df = 1, p-value < 2.2e-16

nrow(Class1_3)

## [1] 707

chies(chi.sq = 95.893, n = nrow(Class1_3))

## Mean Differences ES: 
##  
##  d [ 95 %CI] = 0.79 [ 0.63 , 0.95 ] 
##   var(d) = 0.01 
##   p-value(d) = 0 
##   U3(d) = 78.57 % 
##   CLES(d) = 71.22 % 
##   Cliff's Delta = 0.42 
##  
##  g [ 95 %CI] = 0.79 [ 0.63 , 0.95 ] 
##   var(g) = 0.01 
##   p-value(g) = 0 
##   U3(g) = 78.55 % 
##   CLES(g) = 71.2 % 
##  
##  Correlation ES: 
##  
##  r [ 95 %CI] = 0.37 [ 0.3 , 0.43 ] 
##   var(r) = 0 
##   p-value(r) = 0 
##  
##  z [ 95 %CI] = 0.39 [ 0.31 , 0.46 ] 
##   var(z) = 0 
##   p-value(z) = 0 
##  
##  Odds Ratio ES: 
##  
##  OR [ 95 %CI] = 4.2 [ 3.15 , 5.61 ] 
##   p-value(OR) = 0 
##  
##  Log OR [ 95 %CI] = 1.44 [ 1.15 , 1.72 ] 
##   var(lOR) = 0.02 
##   p-value(Log OR) = 0 
##  
##  Other: 
##  
##  NNT = 3.57 
##  Total N = 707

Auch der letzte Test bestätigt einen Unterschied zwischen Klasse 1 und 3 um den Faktor 3,57.

Visualisierung der Effektstärke

Im nachfolgenden und letzten Schritt sollen die errechneten Effektstärken für die drei Gruppenvergleiche visualisiert werden.

Visualisierung Effektstärke Klasse 1 und 2

Visualization_Class1_2 <- Class1_2 %>% count(Pclass, Survived)
Visualization_Class1_2$proportion <- Visualization_Class1_2$n / nrow(Class1_2)
Visualization_Class1_2

## # A tibble: 4 x 4
##   Pclass Survived     n proportion
##    <int>    <int> <int>      <dbl>
## 1      1        0    80      0.2  
## 2      1        1   136      0.34 
## 3      2        0    97      0.242
## 4      2        1    87      0.218

ggplot(Visualization_Class1_2, aes(x = factor(Pclass), y = n, fill = factor(Survived))) +
  geom_col(position = "fill") +
  ggtitle("Visualization effective strength of Class 1 & 2") + 
  xlab("Class") + 
  ylab("n") +
  guides(fill=guide_legend(title = "Survived?\n0 = No / 1 = Yes"))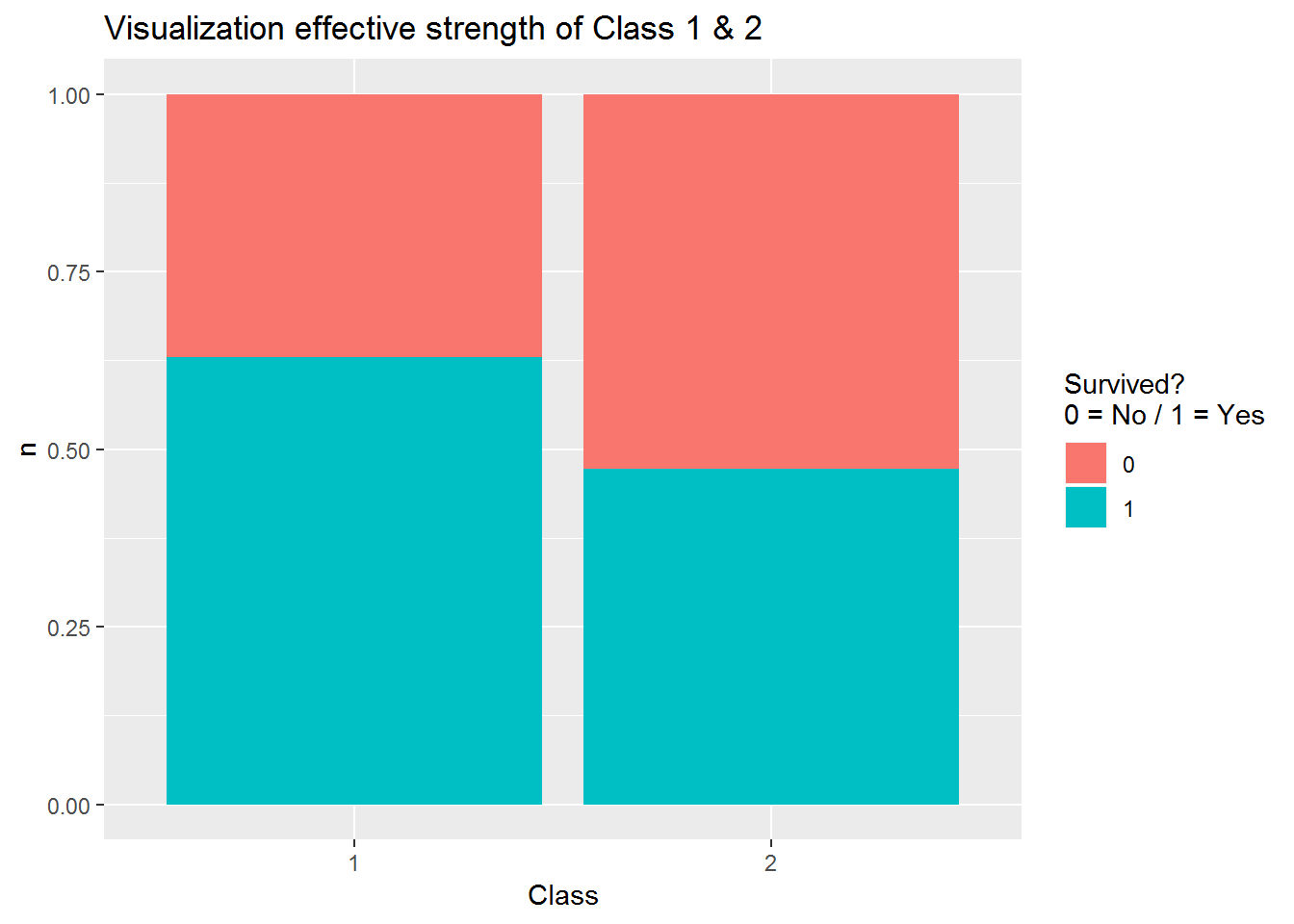

Visualisierung Effektstärke Klasse 2 und 3

Visualization_Class2_3 <- Class2_3 %>% count(Pclass, Survived)
Visualization_Class2_3$proportion <- Visualization_Class2_3$n / nrow(Class2_3)
Visualization_Class1_2

## # A tibble: 4 x 4
##   Pclass Survived     n proportion
##    <int>    <int> <int>      <dbl>
## 1      1        0    80      0.2  
## 2      1        1   136      0.34 
## 3      2        0    97      0.242
## 4      2        1    87      0.218

ggplot(Visualization_Class2_3, aes(x = factor(Pclass), y = n, fill = factor(Survived))) +
  geom_col(position = "fill") +
  ggtitle("Visualization effective strength of Class 2 & 3") + 
  xlab("Class") + 
  ylab("n") +
  guides(fill=guide_legend(title = "Survived?\n0 = No / 1 = Yes"))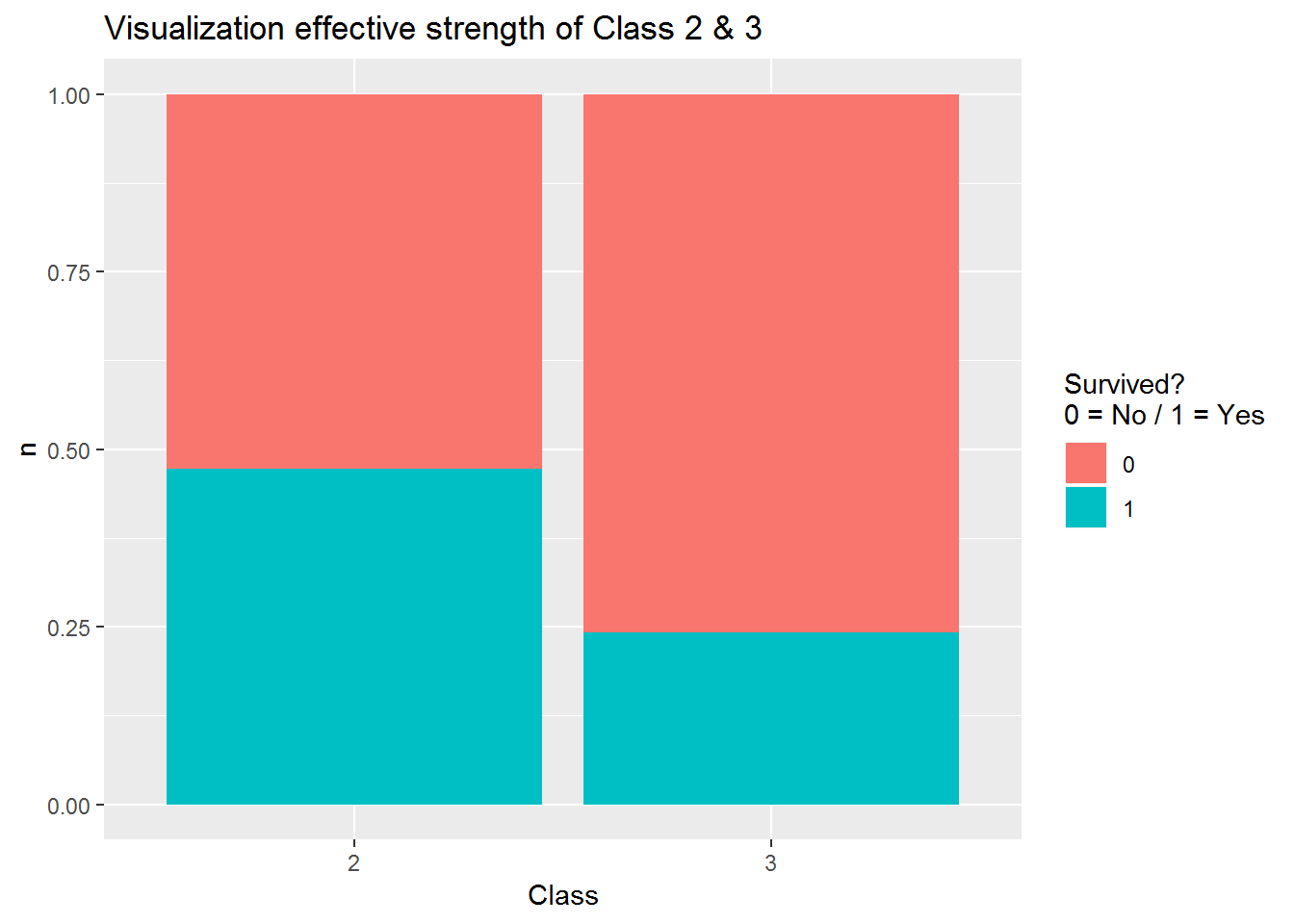

Visualisierung Effektstärke Klasse 1 und 3

Visualization_Class1_3 <- Class1_3 %>% count(Pclass, Survived)
Visualization_Class1_3$proportion <- Visualization_Class1_3$n / nrow(Class1_3)
Visualization_Class1_3

## # A tibble: 4 x 4
##   Pclass Survived     n proportion
##    <int>    <int> <int>      <dbl>
## 1      1        0    80      0.113
## 2      1        1   136      0.192
## 3      3        0   372      0.526
## 4      3        1   119      0.168

ggplot(Visualization_Class1_3, aes(x = factor(Pclass), y = n, fill = factor(Survived))) +
  geom_col(position = "fill") +
  ggtitle("Visualization effective strength of Class 1 & 3") + 
  xlab("Class") + 
  ylab("n") +
  guides(fill=guide_legend(title = "Survived?\n0 = No / 1 = Yes"))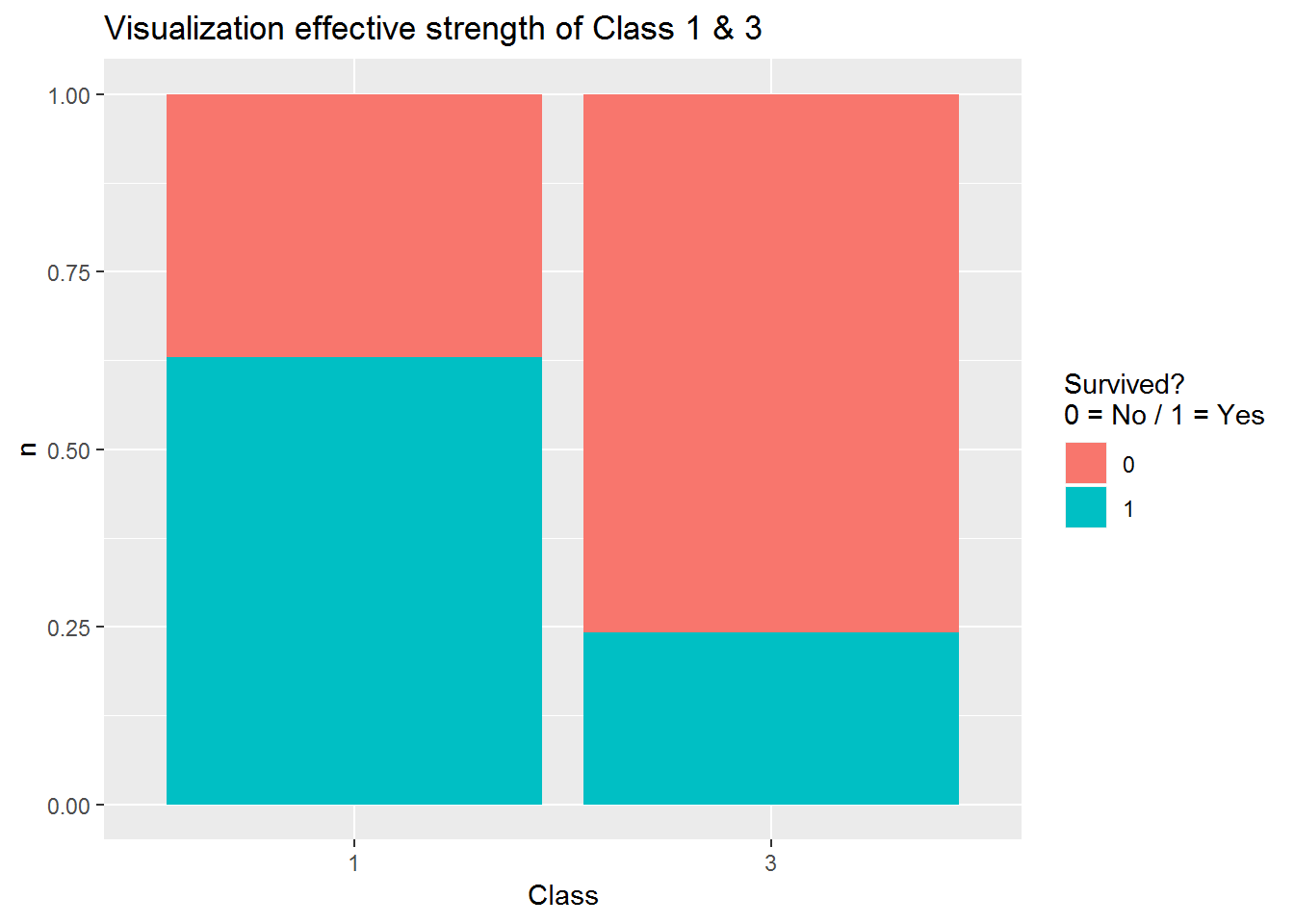

Conclusion

Zwischen allen drei Klassen der Titanic gibt es erhebliche Unterschiede bei der Überlebenschance. Diese Fallstudie soll eine Möglichkeit der Analyse von nominal skalierten Variablen aufzeigen. Dabei lag der Fokus dieser Case Study mehr auf der deskreptiven und explorativen Datenanalyse.

Survive on the Titanic - Case Study